Bài giảng Số học Lớp 6 - Tiết 31: Ứơc chung lớn nhất

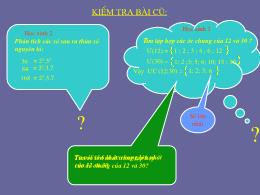
Kiểm tra bài cũ:Tìm tập hợp các ước chung của 12 và 30 ?Ư(12) = 1 ; 2 ; 3 ; 4 ; 6 ; 12Ư(30) = 1; 2 ;3; 5; 6; 10; 15 ; 30Vậy ƯC (12;30) = ?Phân tích các số sau ra thừa số nguyên tố:= 22.32= 22.3.7= 23.3.7Học sinh 1Học sinh 2?36841681; 2; 3; 6Tìm số lớn nhất trong tập hợp các ước chung của 12 và 30?Số lớn nhấtTa nói số 6 là ước chung lớn nhất của 12 và 30Tiết 31: Ước chung lớn nhất 1. Ước chung lớn nhất Ví dụ 1: Tìm ước chung lớn nhất của 12 và 30. Ư(12) = 1 ; 2 ; 3 ; 4 ; 6 ; 12Ư(30) = 1; 2 ;3; 5; 6; 10; 15 ; 30 ƯC (12;30) = 1; 2; 3 ; 6 Vậy 6 là ước chung lớn nhất của 12 và 30Kí hiệu:ƯCLN (12;30) = 6Ta lần lượt tìm:Qua ví dụ trên, em hãy nêu cách tìm ƯCLN của hai hay nhiều số?? Liệt kê các ước của các số đó Chọn ra các ước chung- Tìm ƯCLNQuá dễ Em có nhận xét gì về quan hệ giữa các ƯC ( 12 ; 30 ) với ƯCLN ( 12 ; 30 )? Tất cả các ƯC ( 12 ; 30 ) đều là ước của ƯCLN ( 12 ; 30 )Nhận xét: Tất cả các ước chung của 12 và 30( là 1;2;3;6 ) đều là ước của ƯCLN ( 12 ; 30 ) Nếu tìm được ước chung lớn nhất của hai hay nhiều số ta có tìm được các ước chung của các số đó hay không?Tìm: ƯCLN ( 1 ; 8 )ƯCLN ( 1 ; 2 ; 4 ; 5 ; 10 )Tìm: ƯCLN ( 1 ; 8 ) = 1ƯCLN ( 1 ; 2 ; 4 ; 5 ; 10 ) = 1Thế nào là ƯCLN của hai hay nhiều số ?Các bước tìm ƯCLN: - Liệt kê các ước của các số đó - Chọn ra các ước chung - Tìm ƯCLN* Ước chung lớn nhất của hai hay nhiều số là số lớn nhất trong tập hợp các ước chung của các số đóTiết 31: Ước chung lớn nhất 1. Ước chung lớn nhất Ví dụ 1: Tìm ước chung lớn nhất của 12 và 30. Ư(12) = 1 ; 2 ; 3 ; 4 ; 6 ; 12Ư(30) = 1; 2 ;3; 5; 6; 10; 15 ; 30 ƯC (12;30) = 1; 2; 3 ; 6 6Vậy 6 là ước chung lớn nhất của 12 và 30Kí hiệu:ƯCLN (12;30) = 6Ta lần lượt tìm:?Tìm được chứ!Nhận xét: Tất cả các ước chung của 12 và 30( là 1;2;3;6 ) đều là ước của ƯCLN ( 12 ; 30 )Các bước tìm ƯCLN: - Liệt kê các ước của các số đó - Chọn ra các ước chung - Tìm ƯCLN* Ước chung lớn nhất của hai hay nhiều số là số lớn nhất trong tập hợp các ước chung của các số đó Nếu tìm được ƯCLN của hai hay nhiều số ta có tìm được các ƯC của chúng hay không?Ví dụ: Cho biết: ƯCLN ( 16 ; 40 ) = 8Tìm ƯC ( 16 ; 40 ) ? ƯCLN ( 16 ; 40 ) = 8 nên ƯC ( 16 ; 40 ) là ước của 8Ư(8) = ƯC ( 16 ; 40 ) =Như vậy: Tìm được ƯC Tìm được ƯCLN Tiết 31: Ước chung lớn nhất 1. Ước chung lớn nhất Ví dụ 1: Tìm ước chung lớn nhất của 12 và 30. Ư(12) = 1 ; 2 ; 3 ; 4 ; 6 ; 12Ư(30) = 1; 2 ;3; 5; 6; 10; 15 ; 30 ƯC (12;30) = 1; 2; 3 ; 6 6Vậy 6 là ước chung lớn nhất của 12 và 30Kí hiệu:ƯCLN (12;30) = 6Ta lần lượt tìm:?Nhận xét: Tất cả các ước chung của 12 và 30( là 1;2;3;6 ) đều là ước của ƯCLN ( 12 ; 30 )Tìm: ƯCLN ( 1 ; 8 )ƯCLN ( 1 ; 2 ; 4 ; 5 ; 10 )Tìm: ƯCLN ( 1 ; 8 ) = 1ƯCLN ( 1 ; 2 ; 4 ; 5 ; 10 ) = 1Các bước tìm ƯCLN: - Liệt kê các ước của các số đó - Chọn ra các ước chung - Tìm ƯCLN* Ước chung lớn nhất của hai hay nhiều số là số lớn nhất trong tập hợp các ước chung của các số đóNhư vậy: Tìm được ƯC Tìm được ƯCLN Tìm: - ƯCLN ( 1 ; 8 ) - ƯCLN (1 ; 2; 4; 5; 10 ) ƯCLN ( 1 ; 8 ) = 1 ƯCLN (1 ; 2; 4; 5; 10 ) = 1Chú ý: Số 1 chỉ có một ước là 1. Do đó với mọi số tự nhiên a và b, ta có: ƯCLN ( a ; 1 ) = 1 ƯCLN ( a ; b ; 1) = 1Tiết 31: Ước chung lớn nhất 1. Ước chung lớn nhất ? * Các bước tìm ƯCLN: - Liệt kê các ước của các số đó - Chọn ra các ước chung - Tìm ƯCLN* Ước chung lớn nhất của hai hay nhiều số là số lớn nhất trong tập hợp các ước chung của các số đó2. Tìm ước chung lớn nhất bằng cách phân tích các số ra thừa số nguyên tốVí dụ 2: Tìm ƯCLN ( 36 ; 84 ; 168 )- Phân tích ba số trên ra thừa số nguyên tố: = 22.32= 22.3.7= 23.3.73684168- Chọn ra các thừa số chung.đó là 2 và 3 Lập tích các thừa số vừa chọn, mỗi thừa số lấy với số mũ nhỏ nhất 22. 3ƯCLN( 36 ; 84 ; 168 ) ==12 Dựa vào ví dụ 2. Hãy nêu các bước tìm ƯCLN của hai hay nhiều số lớn hơn 1?B1: Phân tích mỗi số ra thừa số nguyên tố: B2: Chọn ra các thừa số chungB3: Lập tích các thừa số vừa chọn, mỗi thừa số lấy với số mũ nhỏ nhất Các bước tìm ƯCLN:B1: Phân tích ba số trên ra thừa số nguyên tố: B2: Chọn ra các thừa số chungB3: Lập tích các thừa số vừa chọn, mỗi thừa số lấy với số mũ nhỏ nhất Các bước tìm ƯCLN:Tiết 31: Ước chung lớn nhất 1. Ước chung lớn nhất * Các bước tìm ƯCLN: - Liệt kê các ước của các số đó - Chọn ra các ước chung - Tìm ƯCLN* Ước chung lớn nhất của hai hay nhiều số là số lớn nhất trong tập hợp các ước chung của các số đó2. Tìm ước chung lớn nhất bằng cách phân tích các số ra thừa số nguyên tốB1: Phân tích mỗi số ra thừa số nguyên tố: B2: Chọn ra các thừa nguyên tố số chungB3: Lập tích các thừa số vừa chọn, mỗi thừa số lấy với số mũ nhỏ nhất * Các bước tìm ƯCLN:Hoạt động nhóm:Nhóm 1:Nhóm 2:Nhóm 3:Nhóm 4:Tìm ƯCLN (12 ; 30 )Tìm ƯCLN ( 8 ; 9 )Tìm ƯCLN ( 8 ; 12 ; 15 )Tìm ƯCLN (24 ; 16 ; 8 )?1?2Phân tích: 12 = 22..3 30 = 2.3.5Suy ra ƯCLN( 12 ; 30) = 2. 3 = 6Phân tích : 8 = 23.1 9 = 32.1Suy ra ƯCLN ( 8 ; 9 ) = 1Phân tích: 24 = 23. 3 16 = 24 8 = 23 Suy ra ƯCLN ( 24 ; 16 ; 8 ) = 23 = 8 Phân tích: 8 = 23..1 12 = 22. 3.1 15 = 3. 5.1Suy ra ƯCLN ( 8 ; 12 ; 15 ) =1Chú ý: a). Nếu các số đã cho không có thừa số nguyên tố chung thì ƯCLN của chúng bằng 1.Hai hay nhiều số có ƯCLN bằng 1 gọi là các số nguyên tố cùng nhaub). Trong các số đã cho, nếu số nhỏ nhât là ước của các số còn lại thì ƯCLN của các số đã cho chính là số nhỏ nhất ấyTiết 31: Ước chung lớn nhất 1. Ước chung lớn nhất * Các bước tìm: - Liệt kê các ước của các số đó - Chọn ra các ước chung - Tìm ƯCLN* Ước chung lớn nhất của hai hay nhiều số là số lớn nhất trong tập hợp các ước chung của các số đó2. Tìm ước chung lớn nhất bằng cách phân tích các số ra thừa số nguyên tốB1: Phân tích mỗi số ra thừa số nguyên tố: B2: Chọn ra các thừa nguyên tố số chungB3: Lập tích các thừa số vừa chọn, mỗi thừa số lấy với số mũ nhỏ nhất * Các bước tìm:Chú ý: a). Nếu các số đã cho không có thừa số nguyên tố chung thì ƯCLN của chúng bằng 1.Hai hay nhiều số có ƯCLN bằng 1 gọi là các số nguyên tố cùng nhaub). Trong các số đã cho, nếu số nhỏ nhât là ước của các số còn lại thì ƯCLN của các số đã cho chính là số nhỏ nhất ấy3. Cách tìm ước chung thông qua tìm ƯCLN Theo nhận xét ở mục 1: Tất cả các ước chung của 12 và 30 ( là 1;2;3;6 ) đều là ước của ƯCLN (12; 30) ? Qua nhận xét ở mục 1, em hãy nêu Thêm cách tìm ước chung của các số đã cho? Cách tìm:Tìm ƯCLNTìm các ước củaƯCLNTiết 31: Ước chung lớn nhất 1. Ước chung lớn nhất * Các bước tìm: - Liệt kê các ước của các số đó - Chọn ra các ước chung - Tìm ƯCLN* Ước chung lớn nhất của hai hay nhiều số là số lớn nhất trong tập hợp các ước chung của các số đó2. Tìm ước chung lớn nhất bằng cách phân tích các số ra thừa số nguyên tốB1: Phân tích mỗi số ra thừa số nguyên tố: B2: Chọn ra các thừa nguyên tố số chungB3: Lập tích các thừa số vừa chọn, mỗi thừa số lấy với số mũ nhỏ nhất * Các bước tìm:Chú ý: a). Nếu các số đã cho không có thừa số nguyên tố chung thì ƯCLN của chúng bằng 1.Hai hay nhiều số có ƯCLN bằng 1 gọi là các số nguyên tố cùng nhaub). Trong các số đã cho, nếu số nhỏ nhât là ước của các số còn lại thì ƯCLN của các số đã cho chính là số nhỏ nhất ấy3. Cách tìm ước chung thông qua tìm ƯCLN Cách tìm:Tìm ƯCLNTìm các ước củaƯCLNBài tập áp dụng: Bài: 142 Tr 56. Tìm ƯCLN rồi tìm các ước chung củaa). 16 và 24b). 180 và 234 Ta có: 16 = 24 24 = 23. 3Nên ƯCLN(16 ; 24) = 23 = 8 Suy ra ƯC ( 16 ; 24 ) =Ta có: 180 = 22. 32. 5 234 = 2. 32. 13Nên ƯCLN ( 180 ; 234 ) = 2.32 =18Suy ra ƯC ( 180 ; 234 ) =Hướng dẫn về nhà- Nắm chắc được cách tìm ƯCN ( có 2 cách )- Tìm được ƯCLN của các số ta có thể tìm đượ ước chung của các số đóBài tập về nhà:Bài tập: 139 ; 190 ; 143 ; 144 ; 145 ( SGK )Hướng dẫn : Bài: 143( SGK )Tìm số tự nhiên a lớn nhấ, biết rằng 420 a và 700 aGợi ý: a là ƯCLN ( 420 ; 700 ) từ đó ta đi tìm ƯCLN (420 ; 700)Bài 145( SGK ) Lan có một tấm bìa hình chưz nhật kích thước 75 cm và 105 cm. Lan muốn cắt tấm bìa thành các mảnh nhỏ hình vuông bằng nhau sao cho tấm bìa được cắt hết, không còn thừa mảnh nào. Tính độ dài lớn nhất của cạnh hình vuông ( số đo cạnh hình vuông hỏ là xentimet ) Gợi ý: Số đo cạnh hình vông nhỏ là ƯCLN ( 75 ; 105 )