Giáo án Hình học Lớp 7 - Tiết 68: Luyện tập - Năm học 2004-2005
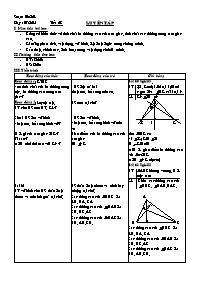
Hoạt động của thầy Hoạt động của trò Ghi bảng
Hoạt động 1: KTBC
Nêu tính chất của ba đường trung trực, ba đường cao trong tam giác?
Hoạt động 2: Luyện tập.
GV cho HS nêu GT, KL?
Cho 1 HS lên vẽ hình
Nhận xét, bổ sung hình vẽ?
M là gì của tam giác INK?
Vì sao?
=>IM như thế nào với KN?
Bài 61
GV vẽ hình cho HS thảo luận nhóm và nếu kết quả tại chỗ.
Bài 62
GV hướng dẫn HS cách vẽ hình.
Để chứng minh tam giác ABC cân (dự đoán tại đâu?) ta phải chúng minh được điều gì?
Muốn vậy ta phải chứng minh điều gì?
Hai tam giác này là tam giác gì? Ta chứng minh bằng nhau theo trường hợp nào?
GV cho HS thảo luận nhóm và đại diện lên trình bày.
Nhận xét (bổ sung nếu có)?
Tương tự vì tam giác đều là tam giác cân tại mấy đỉnh?
Về vận dụng chứng minh trên chứng minh phần còn lại.
1 HS lện trả bài
nhận xét, bổ sung nếu có.
HS nêu tại chỗ
1 HS lên vẽ hình.
Nhận xét, bổ sung hình vẽ nếu có
Giao điểm của ba đường cao của tam giác
IMNK
HS thảo luận nhóm và trình bày miệng tại chỗ.
Các đừng cao của HBC là:
AH, BA, CA
Các đường cao của HAB là:
CH, BC, AC
Các đường cao của HAC là:
BH, AB, CB.
HS vẽ hình
AB = AC hoặc góc B = góc C
BMC = CNB
Vuông
Cạnh huyền cạnh góc vuông.
HS thảo luận nhóm, đại diện lện trình bày.
Nhận xét, bổ sung nếu có. Bài 60 Sgk/83.
GT I, J, Kd; ld tại J; Ml
c qua I và MK cắt l tại N
KL KNIM N
l
M
I J K
Xét INK có
NJIK; KMIN
INKM=M
=>M là giao điểm ba đường cao củaINK
=>IMNK (đpcm)
Bài 61 Sgk/83
GT ABC không vuông. H là
trực tâm
KL Chỉ ra các đường cao của
HBC , HAB, HAC.
A
H
B C
Các đừng cao của HBC là:
AH, BA, CA
Các đường cao của HAB là:
CH, BC, AC
Các đường cao của HAC là:
BH, AB, CB.
Bài 62 Sgk/83
A
N M
B C
Chứng minh
Xét BMC và CNB có
Cạnh huyền BC chung
BM = CN (gt)
=>BMC = CNB (ch-cgv)
=>B = C
=>ABC cân tại A (đpcm)
Soạn: 06/5/Á Dạy : 07/5/05 Tiết 68 LUYỆN TẬP I. Mục tiêu bài học Củng cố kiến thức về tính chất ba đường cao của tam giác, tính chất các đường trong tam giác cân. Kĩ năng phân tích, vận dụng, vẽ hình, lập luận lôgíc trong chứng minh. Cẩn thận, chính xác, linh hoạt trong vận dụng chưnf1 minh. II. Phương tiện dạy học GV: Đddh HS: Đdht III. Tiến trình Hoạt động của thầy Hoạt động của trò Ghi bảng Hoạt động 1: KTBC Nêu tính chất của ba đường trung trực, ba đường cao trong tam giác? Hoạt động 2: Luyện tập. GV cho HS nêu GT, KL? Cho 1 HS lên vẽ hình Nhận xét, bổ sung hình vẽ? M là gì của tam giác INK? Vì sao? =>IM như thế nào với KN? Bài 61 GV vẽ hình cho HS thảo luận nhóm và nếu kết quả tại chỗ. Bài 62 GV hướng dẫn HS cách vẽ hình. Để chứng minh tam giác ABC cân (dự đoán tại đâu?) ta phải chúng minh được điều gì? Muốn vậy ta phải chứng minh điều gì? Hai tam giác này là tam giác gì? Ta chứng minh bằng nhau theo trường hợp nào? GV cho HS thảo luận nhóm và đại diện lên trình bày. Nhận xét (bổ sung nếu có)? Tương tự vì tam giác đều là tam giác cân tại mấy đỉnh? Về vận dụng chứng minh trên chứng minh phần còn lại. 1 HS lện trả bài nhận xét, bổ sung nếu có. HS nêu tại chỗ 1 HS lên vẽ hình. Nhận xét, bổ sung hình vẽ nếu có Giao điểm của ba đường cao của tam giác IMNK HS thảo luận nhóm và trình bày miệng tại chỗ. Các đừng cao của HBC là: AH, BA, CA Các đường cao của HAB là: CH, BC, AC Các đường cao của HAC là: BH, AB, CB. HS vẽ hình AB = AC hoặc góc B = góc C BMC = CNB Vuông Cạnh huyền cạnh góc vuông. HS thảo luận nhóm, đại diện lện trình bày. Nhận xét, bổ sung nếu có. Bài 60 Sgk/83. GT I, J, Kd; ld tại J; Ml c qua I và MK cắt l tại N KL KNIM N l M I J K Xét INK có NJIK; KMIN INKM=M =>M là giao điểm ba đường cao củaINK =>IMNK (đpcm) Bài 61 Sgk/83 GT ABC không vuông. H là trực tâm KL Chỉ ra các đường cao của HBC , HAB, HAC. A H B C Các đừng cao của HBC là: AH, BA, CA Các đường cao của HAB là: CH, BC, AC Các đường cao của HAC là: BH, AB, CB. Bài 62 Sgk/83 A N M B C Chứng minh Xét BMC và CNB có Cạnh huyền BC chung BM = CN (gt) =>BMC = CNB (ch-cgv) =>B = C =>ABC cân tại A (đpcm) Hoạt động 3: Dặn dò Về xem kĩ lại lý thuyết và các dạng bài tập đã làm. Xem lại toàn bộ lý thuyết của chương tiết sau ôn tập chương. BTVN: 63, 64, 65 Sgk/87 Ôn các câu hỏi lý thuyết.
Tài liệu đính kèm:
 Tiet 68.doc
Tiet 68.doc





