Giáo án Hình học Lớp 7 - Tiết 66: Luyện tập - Năm học 2004-2005
Hoạt động của thầy Hoạt động của trò Ghi bảng
Hoạt động 1: KTBC
Hãy phát biểu 2 tính chất về đường trung trực của một đoạn thẳng?
Hoạt động 2: Luyện tập.
Bài 54 GV cho 3 HS lên vẽ
GV hướng dẫn trứoc khi HS thực hiện: Đường tròn đi dua ba đỉnh nghĩa là tâm đường tròn như thế nào với ba đỉnh?
Bài 55
GV treo bảng phụ cho HS quan sát
Để B, D, C thẳng hàng thì góc BDC bằng bao nhiêu độ?
Vậy ta sẽ chứng minh tổng hai góc nào bằng 1800?
Góc BDI ? IDA; ADK ? CDK vì sao?
Mà góc IDA + KDA =? Độ?
=> góc BDI+CDA =? Độ?
Vậy => góc BDC =? Tổng những góc nào và bằng bao nhiêu độ?
Ta thấy ID ? AC; KD? AB theo tính chất gì?
=>Dlà gì của BC?
Mặt khác ID và KD còn là gì của AB và AC?
=>Kết luận nhhư thế nào?
GV Từ nay các em coi đây như là một định lý để vận dụng trong chứng minh.
1 HS lên trả bài
HS nhận xét.
3 HS lên vẽ hình.
1800
tổng hai góc ADB + ADC = 1800
bằng nhau vì ID, KD là hai trung trực nên tam giác BDA và ADC cân tại D
900
900
Bằng tổng các góc IDA + KDA +BDI+CDA = 1800
// = ½
trung điểm của BC
trung trực của AB và BC
HS nêu nên kết luận.
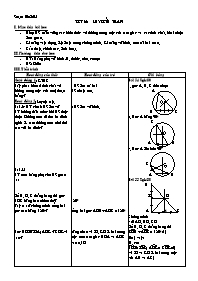
Bài 54 Sgk/80
a. góc A, B, C đều nhọn
A
B C
b. Góc A bằng 900
C
A B
c. Góc A lớn hơn 900
C
A B
Bài 55 Sgk/80
B
I D
A K C
Chứng minh
Nối AD, BD, CD
Để B, D, C thẳng hàng thì
ADB + ADC = 1800 (1)
Thật vậy:
Ta có:
BDI = IDA; ADK = CDK (2)
(vì ID và KD là hai trung trực của AB và AC)
Mà IDKD tại D
=> IDA + KDA = 900
Từ (2) =>BDI+CDA = 900
Mặt khác
BDC =IDA + KDA +BDI+CDA
= 900+900 = 1800
=> BDC là góc bẹt hay B, D, C thẳng hàng.
Bài 56 Sgk/80
Chứng minh điểm cách đều ba đỉnh của một tam giác vuông là trung điểm của cạnh huyền.
Theo bài 55 ta có:
ID//= ½ AC, KD//= ½ AB
Nên ID và KD là đường trung bình của tam giác
=> D là trung điểm của BC
Mặt khác ID và KD là hai đường trung trực nên D cũng là điểm cách đều ba đỉnh của tam giác.
Soạn: 03/5/05 Tiet 66 Luyeenj taapj I. Mục tiêu bài học Giúp HS nắm vững các kiến thức về đường trung trực của tam giác và các tính chất, khái niệm liên quan. Kĩ năng vận dụng, lập luận trong chứng minh. Kĩ năng vẽ hình, tóm tắt bài toán. Cẩn thận, chính xác, linh hoạt. II. Phương tiện dạy học GV: Bảng phụ vẽ hình 51, thước, êke, compa HS: Đdht III. Tiến trình Hoạt động của thầy Hoạt động của trò Ghi bảng Hoạt động 1: KTBC Hãy phát biểu 2 tính chất về đường trung trực của một đoạn thẳng? Hoạt động 2: Luyện tập. Bài 54 GV cho 3 HS lên vẽ GV hướng dẫn trứoc khi HS thực hiện: Đường tròn đi dua ba đỉnh nghĩa là tâm đường tròn như thế nào với ba đỉnh? Bài 55 GV treo bảng phụ cho HS quan sát Để B, D, C thẳng hàng thì góc BDC bằng bao nhiêu độ? Vậy ta sẽ chứng minh tổng hai góc nào bằng 1800? Góc BDI ? IDA; ADK ? CDK vì sao? Mà góc IDA + KDA =? Độ? => góc BDI+CDA =? Độ? Vậy => góc BDC =? Tổng những góc nào và bằng bao nhiêu độ? Ta thấy ID ? AC; KD? AB theo tính chất gì? =>Dlà gì của BC? Mặt khác ID và KD còn là gì của AB và AC? =>Kết luận nhhư thế nào? GV Từ nay các em coi đây như là một định lý để vận dụng trong chứng minh. 1 HS lên trả bài HS nhận xét. 3 HS lên vẽ hình. 1800 tổng hai góc ADB + ADC = 1800 bằng nhau vì ID, KD là hai trung trực nên tam giác BDA và ADC cân tại D 900 900 Bằng tổng các góc IDA + KDA +BDI+CDA = 1800 // = ½ trung điểm của BC trung trực của AB và BC HS nêu nên kết luận. Bài 54 Sgk/80 a. góc A, B, C đều nhọn A B C b. Góc A bằng 900 C A B c. Góc A lớn hơn 900 C A B Bài 55 Sgk/80 B I D A K C Chứng minh Nối AD, BD, CD Để B, D, C thẳng hàng thì ADB + ADC = 1800 (1) Thật vậy: Ta có: BDI = IDA; ADK = CDK (2) (vì ID và KD là hai trung trực của AB và AC) Mà IDKD tại D => IDA + KDA = 900 Từ (2) =>BDI+CDA = 900 Mặt khác BDC =IDA + KDA +BDI+CDA = 900+900 = 1800 => BDC là góc bẹt hay B, D, C thẳng hàng. Bài 56 Sgk/80 Chứng minh điểm cách đều ba đỉnh của một tam giác vuông là trung điểm của cạnh huyền. Theo bài 55 ta có: ID//= ½ AC, KD//= ½ AB Nên ID và KD là đường trung bình của tam giác => D là trung điểm của BC Mặt khác ID và KD là hai đường trung trực nên D cũng là điểm cách đều ba đỉnh của tam giác. Hoạt động 3: Dặn dò Về học kĩ lý thuyết và các dạng bài tập đã làm. Chuẩn bị trước bài 9 tiết sau học: Giấy cắt hình tam giác sẵn. BTVN: bài 55 Sgk/80
Tài liệu đính kèm:
 Tiet 66.doc
Tiet 66.doc





