Tài liệu môn Vật lý - Một số phương pháp giải bài toán mạch cầu điện trở
Bài toán 1;
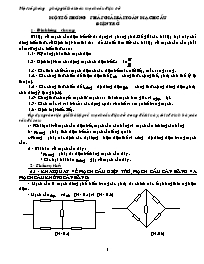
Cho mạch cầu điện trở như (H - 1.1)
1 - Chứng minh rằng, nếu qua R5 có dòng
I5 = 0 và U5 = 0 thì các điện trở nhánh lập
thành tỷ lệ thức :
(H : 1-1)
= n = const
2 - Ngược lại nếu có tỷ lệ thức trên
thì I5 = 0 và U5 = 0, ta có mạch cầu cân bằng.
3- Chứng minh rằng khi có tỷ lệ thức trên thì điện trở tương đương của mạch cầu không tuỳ thuộc vào giá trị R5 từ đó tính điện trở tương đương của mạch cầu trong hai trường hợp R5 nhỏ nhất ( R5 = 0) và R5 lớn nhất (R5 = ) để I5 = 0 và U5 = 0, ta có mạch cầu cân bằng.
Lời giải
1- Gọi I1; I2; I3; I4; I5 lần lượt là cường độ dòng điện qua các điện trở R1; R2; R3; R4; R5.
Và U1; U2; U3; UBND; U5 lần lượt là hiệu điện thế ở hai đầu các điện trở R1; R2; R3; R4; R5.
Theo đầu bài:
I5 = 0 suy ra: I1 = I2 = I 1,2 và I3 = I4 = I 34 (1)
U5 = 0 suy ra: U1 = U2 và U2 = U4.
Hay I1R1 = I3R3 (2)
I2R2 = I4R4 (3)
Lấy (2) chia (3) vế với vế, rồi kết hợp với (1) ta được :
hay= n = const
2- Dùng định lý Kennơli, biến đổi mach tam giác thành mạch sao:
-Ta có mạch điện tương đương như hình vẽ : (H: 1 -2)
Trong đó các điện trở R1; R2; R3
được thay bằng các đoạn mạch sao
gồm các điện trở R1; R3 và R5
Với:
(H:1.2)
- Xét đoạn mạch MB có:
(5)
(6)
Chia (5) cho (6) vế với vế ta được :
(7)
Từ điều kiện đầu bài ta có:
R1 = n R3; R2 = n R4
Thay vào biểu thức (7) ta được :
Hay : U2 = U4 Suy ra UCD = U5 = 0 => I5 = 0
Nghĩa là mạch cầu cân bằng.
Một số phương pháp giải bài toán mạch cầu điện trở 1 - Định hướng chung: Bài tập về mạch cầu điện trở rất đa dạng và phong phú. Để giải các bài tập loại này chỉ dùng kiến thức về Định luật ôm thì chưa đủ. Muốn làm tốt các bài tập về mạch cầu cần phải nắm vững các kiến thức sau: 1.1 - Kỹ năng phân tích mạch điện 1.2 - Định luật ôm cho động mạch có điện trở R: I= 1.3 - Các tính chất của mạch điện có các điện trở mác nối tiếp, mắc song song. 1.4 - Các công thức biến đổi hiệu điện thế ( như công thức cộng thế, phép chia thế tỷ lệ thuận). 1.5 - Các công thức biến đổi cường độ dòng điện (như công thức cộng dòng điện, phép chia dòng ỷ lệ nghịch). 1.6 - Công thức chuyển mạch từ mạch sao thành mạch tam giác và ngược lại. 1.7 - Cách mắc và vai trò của các dụng cụ đo vôn kế va am pe kế trong mạch. 1.8 - Định luật kiếc Sốp. áp dụng vào việc giải bài tập về mạch cầu điện trở trong đề tài này, tôi sẽ trình bày các vấn đề sau: a- Khái quát về mạch cầu điện trở, mạch cầu cân bằng và mạch cầu không cân bằng b- Phương pháp tích điện trở của mạch cầu tổng quát. c-Phương pháp xác định các đại lượng hiệu điện thế và cường độ dòng điện trong mạch cầu. d - Bài toán về mạch cầu dây: * Phương pháp đo điện trở băng mạch cầu dây. * Các loại bài toán thường gặp về mạch cầu dây. 2 - Phần cụ thể: 2.1 - Khái quát về mạch cầu điện trở, mạch cầu cân bằng và mạch cầu không cân bằng: - Mạch cầu là mạch dùng phổ biến trong các phép đo chính xác ở phòng thín nghiệm điện. - Mạch cầu được vẽ như (H - 0.a) và (H - 0.b) (H-0.a) (H.0.b) - Các điện trở R1, R2, R 3, R4 gọi là các cạnh của mạch cầu điện trở R5 có vai trò khác biệt gọi là đường chéo của mạch cầu (người ta không tính thêm đường chéo nối giữa A - B. vì nếu có thì ta coi đường chéo đó mắc song song với mạch cầu). Mạch cầu có thể phân làm hai loại: * Mạch cầu cân bằng (Dùng trong phép đo lường điện). * Mạch cầu không cân bằng Trong đó mạch cầu không cân bằng được phân làm 2 loại: - Loại có một trong 5 điện trở bằng không (ví dụ một trong 5 điện trở đó bị nối tắt, hoặc thay vào đó là một ampe kế có điện trở ằng không ). Khi gặp loại bài tập này ta có thể chuyển mạch về dạng quen thuộc, rồi áp dụng định luật ôm để giải. - Loại mạch cần tổng quát không cân bằng có đủ cả 5 điện trở, thì không thể giải được nếu ta chỉ áp dụng định luật Ôm, loại bài tập này được giải bằng phương pháp đặc biệt (được trình bày ở mục 2.3) - Vậy điều kiện để cân bằng là gì? Bài toán 1; Cho mạch cầu điện trở như (H - 1.1) 1 - Chứng minh rằng, nếu qua R5 có dòng I5 = 0 và U5 = 0 thì các điện trở nhánh lập thành tỷ lệ thức : (H : 1-1) = n = const 2 - Ngược lại nếu có tỷ lệ thức trên thì I5 = 0 và U5 = 0, ta có mạch cầu cân bằng. 3- Chứng minh rằng khi có tỷ lệ thức trên thì điện trở tương đương của mạch cầu không tuỳ thuộc vào giá trị R 5 từ đó tính điện trở tương đương của mạch cầu trong hai trường hợp R5 nhỏ nhất ( R5 = 0) và R5 lớn nhất (R5 = Ơ) để I5 = 0 và U5 = 0, ta có mạch cầu cân bằng. Lời giải 1- Gọi I1; I2; I3; I4; I5 lần lượt là cường độ dòng điện qua các điện trở R1; R2; R3; R4; R5. Và U1; U2; U3; UBND; U5 lần lượt là hiệu điện thế ở hai đầu các điện trở R1; R2; R3; R4; R5. Theo đầu bài: I5 = 0 suy ra: I1 = I2 = I 1,2 và I3 = I4 = I 34 (1) U5 = 0 suy ra: U1 = U2 và U2 = U4. Hay I1R 1 = I3R3 (2) I2R2 = I4R4 (3) Lấy (2) chia (3) vế với vế, rồi kết hợp với (1) ta được : hay= n = const 2- Dùng định lý Kennơli, biến đổi mach tam giác thành mạch sao: -Ta có mạch điện tương đương như hình vẽ : (H: 1 -2) Trong đó các điện trở R1; R2; R3 được thay bằng các đoạn mạch sao gồm các điện trở R1; R3 và R5 Với: (H:1.2) - Xét đoạn mạch MB có: (5) (6) Chia (5) cho (6) vế với vế ta được : (7) Từ điều kiện đầu bài ta có: R1 = n R3; R2 = n R4 Thay vào biểu thức (7) ta được : Hay : U2 = U4 Suy ra UCD = U5 = 0 => I5 = 0 Nghĩa là mạch cầu cân bằng. 3- Giả sử qua R5 có dòng điện I5 đi từ C đến D , (H: 1-3) Ta có: I2 = I1 = I5 và I4 = I 3 + I5 - Biểu diễn hiệu điện thế U theo hai đường ACB và ADB ta có: UACB = U = I1R1 + I2R2 = I1R1 + I1R2 - I5R 2 (8) UADB = U = I3R3 + I4R4 = I3R3 + I3R4 - I5R 4 (9) Nhân hai vế của biểu thức (9) với n ta được : n. U = I3R3 n + I3R4 .n + I5R4 . n Kết hợp điều kiện đầu bài : R1 = n.R3 và R2 = n. R4 Ta có: n.U = I3R1 + I3R3 +: I5R5 (10) Cộng (8) với (10) vế với vế ta được: (n +1) U = R1 (I1 + I3) + R2 (I1 + I3). = (R1 + R2) (I1 + I2). Với I1 + I 3 = I => (n +1) U = (R1 + R2) Theo định nghĩa, điện trở tương đương được tính bằng: (11) Biểu thức (11) cho thấy khi có tỷ lệ thức : Thì điện trở tương đương của mạch cầu không phụ thuộc vào điện trở R5 * Trường hợp R5 = 0 (nối dây dẫn hay ampekế có điện trở không đáng kể, hay một khoá điện đang đóng giữa hai điểm C, D). - Khi đó mạch điện (R1 // R 3), nối tiếp R2 // R4. -> ta luôn có hiệu điện thế UCD = 0. + Điện trở tương đương: sử dụng điều kiện đầu bài R1 = n.R3và R2 = n.R4 ta vẫn có Do R1 // R3 nên: => (12) Do R2 // R4 nên : => (13) So sánh (12) và (13), suy ra I1 = I2 Hay I5 = I - I2 = 0 * Trường hợp R5 = Ơ (đoạn CD để hở hay nối với vôn kế có điện trở lớn vô cùng). - Khi đó mạch điện : (R1 . n + R2) // (R3 . n + R4). -> luôn có dòng điện qua CD là I5 = 0 + Điện trở tương đương. Kết hợp điều kiện đầu bài R1 = n R3 và R2 = n R4 ta cũng có kết quả: . + Do R1 nối tiếp R2 nên : (14) Do R3 nối tiếp R4 nên : (15) So sánh (14) và (15), suy ra U1 = U3 Hay U5 = UCD = U3 -U1 = 0 Vậy khi có tỷ lệ thức: Thì với mọi giá trị của R5 từ o đến Ơ, điện trở tương đương chỉ có một giá trị. Dù đoạn CD có điện trở bao nhiêu đi nữa ta cũng có UCD = và ICD = 0, nghĩa là mạch cầu cân bằng. Tóm lại: Cần ghi nhớ + Nếu mạch cầu điện trở có dòng I5 = 0 và U5 = 0 thì bốn điện trở nhánh của mạch cầu lập thành tỷ lệ thức: (n là hằng số) (*) (Với bất kỳ giá trị nào của R5.). Khi đó nếu biết ba trong bốn điện trở nhánh ta sẽ xác định được điện trở còn lại. * Ngược lại: Nếu các điện trở nhánh của mạch cầu lập thành tỷ lệ thức tên, ta có mạch cầu cân bằng và do đó I5 = 0 và U5 = 0. + Khi mạch cầu cân bằng thì điện trở tương đương của mạch luôn được xác định và không phụ thuộc vào giá trị của điện trở R5 . Đồng thời các đại lượng hiệu điện thế và không phụ thuộc vào điện trở R5 . Lúc đó có thể coi mạch điện không có điện trở R5 và bài toán được giải bình thường theo định luật ôm. + Biểu thức (*) chính là điều kiện để mạch cầu cân bằng. Lưu ý: Học sinh lớp 9 có thể áp dụng công thức của mạch cầu cân bằng mà không cần phải chứng minh (mặc dù SGK không trình bày). + Tuy nhiên khi bồi dưỡng học sinh giỏi ở phần này, giáo viên cần phải chứng minh bài toán trên để học sinh thấy rõ các tính chất của mạch cầu cân bằng. + Mạch cầu cân bằng được dùng để đo giá trị điện trở của vật dẫn (sẽ trình bày cụ thể ở phần sau). 2 .2 - Phương pháp tính điện trở tương đương của mạch cầu: - Tính điện trở tương đương của một mạch điện là một việc làm cơ bản và rất quan trọng, cho dù đầu bài có yêu cầu hay không yêu cầu, thì trong quá trình giải các bài tập điện ta vẫn thường phải tiến hành công việc này. Với các mạch điện thông thường, thì đều có thể tính điện trở tương đương bằng một trong hai cách sau. + Nếu biết trước các giá trị điện trở trong mạch và phân tích được sơ đồ mạch điện (thành các đoạn mắc nối tiếp, các đoạn mắc song song) thì áp dụng công thức tính điện trở của các đoạn mắc nối tiếp hay các đoạn mắc song song. + Nếu chưa biết hết các giá trị của điện trở trong mạch, nhưng biết được Hiệu điện thế ở 2 đầu đoạn mạch và cường độ dòng điện qua đoạn mạch đó, thì có thể tính điện trở tương đương của mạch bằng công thức định luật Ôm. - Tuy nhiên với các mạch điện phức tạp như mạch cầu, thì việc phân tích đoạn mạch này về dạng các đoạn mạch mới nối tiếp và song song là không thể được. Điều đó cũng có nghĩa là không thể tính điện trở tương đương của mạch cầu bằng cách áp dụng, các công thức tính điện trở của đoạn mạch mắc nối tiếp hay đoạn mạch mắc song song. Vậy ta phải tính điện trở tương đương của mạch cầu bằng cách nào? * Với mạch cầu cân bằng thì ta bỏ qua điện trở R5 để tính điện trở tương đương của mạch cầu. * Với loại mạch cầu có một trong 5 điện trở bằng 0, ta luôn đưa được về dạng mạch điện có các đoạn mắc nối tiếp, mắc song song để giải. * Loại mạch cầu tổng quát không cân bằng thì điện trở tương đương được tính bằng các phương pháp sau: 1 - Phương pháp chuyển mạch: Thực chấtl à chuyển mạch cầu tổng quát về mạch điện tương đương (điện trở tương đương của mạch không thay đổi). Mà với mạch điện mới này ta có thể áp dụng các công thức tính điện trở của đoạn mạch nối tiếp, đoạn mạch song song để tính điện trở tương đương. - Muốn sử dụng phương pháp này trước hết ta phải nắm được công thức chuyển mạch (chuyển từ mạch sao thành mạch tam giác và ngược lại từ mạch tam giác thành mạch sao) Công thức chuyển mạch - Định lý Kennơli. + Cho hai sơ đồ mạch điện, mỗi mạch điện được tạo thành từ ba điện trở (H21-a mạch tam giác (D)) A’ (H.21b - Mạch sao (Y) A R’3 R1 R2 R’2 R’1 B C B’ C’ (H - 2.1a) (H- 2.1b) Với các giá trị thích hợp của điện trở có thể thay thế mạch này bằng mạch kia, khi đó hai mạch tương đương nhau. Công thức tính điện trở của mạch này theo mạch kia khi chúng tương đương nhau như sau: * Biến đổi từ mạch tam giác R1, R2, R3 thành mạch sao R’1, R’2, R’3 (1) (2) (3) (ở đây R’1, R’2, R’3 lần lượt ở vị trí đối diện với R1,R2, R3) * Biến đổi từ mạch sao R’1, R’2, R’3 thành mạch tam giác R1, R2, R3 (4) (5) (6) (Do giới hạn không cho phép, nên đề tài này chỉ được ra công thức mà không chứng minh công thức đó !). - áp dụng vào bài toán tính điện trở tương đương của mạch cầu ta có hai cách chuyển mạch như sau: * Cách 1: Từ sơ đồ mạch cầu tổng quát ta chuyểnmạch tam giác R1, R3, R5 thànhm ạch sao :R’1; R’3; R’5 (H- 22a) Trong đó các điện trở R13, R15, R35 được xác định theo công thức: (1); (2) và (3)(H: 2.2a) từ sơ đồ mạch điện mới (H - 22a) ta có thể áp dụng công thức tính điện trở của đoạn mạch mắc nối tiếp, đoạn mạch mắc song song để tính điện trở tương đương của mạch AB, kết quả là: * Cách 2: Từ sơ đồ mạch cầu tổng quát ta chuyển mạch sao R 1, R2 , R5 thành mạch tam giác R’1, R’2 , R’3 (H - 2.2b) Trong đó các điện trở R’1, R’2 , R’3 được xác định theo công thức (4), (5) và (6) (H:2.2b) Từ sơ đồ mạch điện mới (H - 2.2b) áp dụng công thức tính điện trở tương đương ta cũng được kết quả: 2 - Phương pháp dùng công thức đ ... tập điện một chiều, thì nhất thiết giáo viên phải hướng dẫn các em hiểu và vận dụng tốt cả 5 phương phương pháp trên. Các phương pháp đó không chỉ phục vụ cho việc ôn thi học sinh giỏi vật lý lớp 9 mà cả chương trinhf vật lý lớp 11 và ôn thi đại học cũng gặp rất nhiều bài tập phải áp dụng các phương pháp này mơí giải được. 2.4- Bài toán cầu dây: - Mạch cầu dây là mạch điện có dạng như hình vẽ (H - 4.1) Trong đó hai điện trở R3 và R4có giá trị thay đổi khi con chạy C dịch chuyển dọc theo chiều dài của biến trở (R3 = RAC; R4 = RCB) (H-4.1) + Mạch cầu dây được ứng dụng để đo điện trở của 1 vật dẫn. - các bài tập về mạch cầu dây rất đa dạng; phức tạp và p hổ biến trong chương trình Vật lý nâng cao lớp 9 và lớp 11. Vậy sử dụng mạch cầu dây để đo điện trở như thế nào? Và phương pháp để giải bài tập về mạch cầu dây như thế nào? 2.4.1 - Phương pháp đo điện trở của vật dẫn bằng mạch cầu dây: Bài toán 4: Để đo giá trị của điện trở Rx người ta dùng một điện trở mẫu Ro, một biến trở ACB có điện trở phân bố đều theo chiều dài, và một điện kế nhạy G, mắc vào mạch như hình vẽ (H - 4.2) Di chuyển con chạy C của biến trở đến khi điện kế G chỉ số 0 đo l1 ; l2 ta được kết quả: (H-4.2) hãy giải thích phép đo này? Lời giải Trên sơ đồ mạch điện, con chạy C chia biến trở (AB) thành hai phần. + Đoạn AC có chiều dài l1, điện trở là R1 + Đoạn CB có chiều dài l2, điện trở là R2 - Điện kế cho biết khi nào có dòng điện chạy qua đoạn dây CD. Nếu điện kế chỉ số 0, thì mạch cầu cân bằng, khi đó điện thế ở điểm C bằng điện thế ở điểm D. Do đó: VA - VD = VA - VC Hay UAn= UAC => R0I0 = R4 I1 Ta được: (1) (Với I0, I1 lần lượt là dòng điện qua R0 và R4) + Tương tự: UAB = UCB => Rx .I0 = R2 . I2 Hay (2) + Từ (1) và (2) (3) - Vì đoạn dây AB là đồng chất, có tiết diện đều nên điện trở từng phàn được tính theo công thức. và Do đó: (4) - Thay (4) vào (3) ta được kết quả: Chú ý: Đo điện trở của vật dẫn bằng phương pháp trên cho kết quả có độ chính xác rất cao và đơn giản nên được ứng dụng rộng rãi trong phòng thí nghiệm 2.4.2 - Các bài toán thường gặp về mạch cầu dây: Bài toán 5: Cho mạch điện như hình vẽ (H- 4.3) Điện trở của am pe kế và dây nối không đáng kể, điện trở toàn phần của biến trở . a- Tìm vị trí ucả con chạy C khi biết số chỉ của ampekế (IA) b- Biết vị trí con chạy C, tìm số chỉ của ampe kế? * Phương pháp giải: (H- 4.3) Vì điện trở của ampe kế không đáng kể -> mạch điện (R1//RAC) nt (R2 // RCB) a- Đặt x = RAC (0< x< R) * Trường hợp 1: Nếu bài toán cho biết số chỉ của ampe kế IA = 0 Thì mạch cầu cân bằng, lúc đó ta có điều kiện cân bằng. (1) Giải phương trình (1) ta sẽ tìm được RAC = x * Trường hợp 2: Am pe kế chỉ giá trị IA ạ 0 Viết phương trình dòng điện cho hai nút C và D. Rồi áp dụng định luật ôm để chuyển hai phương trình đó về dạng có ẩn sóo là U1 và x. + Nút C cho biết hay (2) + Nút D cho biết: IA = ờI1 - I2ờ hay (3) (Trong đó các giá trị U, Ia, R, R1, R2 đầu bài cho trước ) - Xét chiều dòng điện qua ampe kế (nếu đầu bài không cho trước), để giải phương trình (3) tìm giá trị U1, rồi thay vào phương trình (2) để tìm x. - Từ giá trị của x ta tìm được vị trí tương ứng con chạy C. b- Vì đầu bài cho biết vị trí con chạy C, nên ta xác định được điện trở RAC và RCB - Mạch điện: (R// RAC ) nt (R2 //RCB) -> áp dụng định luật ôm ta dễ dàng tìm được I1và I2. Suy ra số chỉ của Ampe kế: IA = ờI1 - I2 ờ * Bài tập áp dụng: Cho mạch điện như hình vẽ (H - 4.4) Biết U = 7V không đổi. R1 = 3W, R2= 6W Biến trở ACB là một dây dẫn Có điện trở suất là d= 4.106 (W m) Chiều dài l = AB = 1,5m Tiết diện đều: S = 1mm2 a - Tính điện trở toàn phần của biến trở b- Xác định vị trí con chạy C để số chỉ của ampe kế bằng 0 c- Con chạy C ở vị trí mà AC = 2CB, hỏi lúc đó ampe kế chỉ bao nhiêu? d - Xác định vị trí con chạy C để ampe kế chỉ (A) Lời giải a- Điện trở toàn phần của biến trở (W) b- Ampe kế chỉ số 0 thì mạch cầu cân bằng, khi đó Đặt x = RAC -> RCB = 6 -x Suy ra x = 2 (W) Với RAC = x = 2W thì con chạy C ở cách A một đoạn bằng Vậy khi con chạy C cách A một đoạn bằng 0,5m thì ampe kế chỉ số 0 c- Khi con chạy ở vị trí mà AC = 2CB, ta dễ dàng tính được RAC = 4 (W) Còn RCB = 2 (W) VT RA = 0 => Mạch điện (R1 //RAC ) nt (R2 //RCB) - Điện trở tương đương của mạch (W) - Cường độ dòng điện trong mạch chính Suy ra: Vì: I1 > I2, suy ra số chỉ của ampe kế là: hay IA = 0,7 (A) Vậy khi con chạy C ở vị trí mà AC - 2CB thì ampe kế chỉ 0,7 (A) d- Tìm vị trí con chạy C để ampe kế chỉ (A) - Vì: RA = 0 => mạch điện (R1// RAC) nt (R2 // RCB) suy ra: Ux = U1 + Phương trình dòng điện tại nút C: hay (1) + Phương trình dòng điện tại nút D: hay (2) + Trường hợp 1: Ampe kế chỉ IA = (A) D đến C - Từ phương trình (2) ta tìm được U1 = 3 (V) - Thay U1 = 3 (V) vào phương trình (1) ta tìm được x = 3 (W) - Với RAC = x = 3 W ta tìm được vị trí của con chạy C cách A một đoạn bằng AC = 75 (m) + Trường hợp 2: Ampe kế chỉ IA = (A) chiều từ C đến D - Từ phương trình (2) ta tìm được U1 - Thay U1 vào phương trình (1) ta tìm được x ằ 1,16 (W) - Với RAC = x = 1,16 W , ta tìm được vị trí của con chạy C cách A một đoạn bằng AC ằ 29 (cm) Vâỵ tại các vị trí mà con chạy C cách A một đoạn bằng 75 (cm) hoặc 29 (cm) thì am pe kế chỉ . Bài toán 6: Cho mạch điện như hình vẽ (H -4.5) Hiệu điện thế ở hai đầu đoạn mạch là U Không đổ.Biểntở có điện toàn phần là R Vôn kế có điện trở rất lớn (H-4.5) a- Tìm vị trí con chạy C, khi biết số chỉ của vôn kế b- Biết vị trí con chạy C, tìm số chỉ của vôn kế * Phương pháp giải: - Vì vôn kế có điện trở rất lớn nên mạch điện có dạng (R1 nt R2) // RAB a- Tìm vị trí con chạy C - Với mọi vị trí của C, ta luôn tìm được và - Xét hai trường hợp: UAC = U1 + UV và UAC = U1 - UVư Mỗi trường hợp ta luôn có: Từ giá trị của RAC ta tìm được vị trí tương ứng của con chạy C. b- Biết vị trí con chạy C, ta dễ dàng tìm được RAC và RCB và cũng dễ dàng tính được U1 và UAC. Từ đó chỉ số của vôn kế: * Bài tập áp dụng: Cho mạch điện như hình vẽ (H. 4 . 6) Biết V = 9V không đổi, R1 = 3W, R2 = 6W. Biến trở ACB có điện trở toàn phần là R= 18W Vốn kế là lý tưởng. (H- 4.6) a- Xác định vị trí con chạy C để vôn kế chỉ số 0 b- Xác định vị trí con chạy C để vôn kế chỉ số 1vôn c- Khi RAC = 10W thì vôn kế chỉ bao nhiêu vôn ? Lời giải - Vì vôn kế là lý tưởng nên mạch điện có dạng: (R1 nt R2) // RAB a- Để vôn kế chỉ số 0, thì mạch cầu phải cân bằng, khi đó: Hay => RAC = 6 (W) b- Xác định vị trí con chạy C, để Uv = 1(V) - Với mọi vị trí của con chạy C, ta luôn có Và + Trường hợp 1: Vôn kế chỉ: UV = U1 - UAC = 1 (V) Suy ra: UAC = U 1 - UV = 3 - 1 = 2 (V) => RAC = (W) + Trường hợp 2: Vôn kế chỉ UV = UAC - U1 = 1 (V) Suy ra: UAC = U1 + UV = 3 + 1 = 4 (V) => = 8 (W) Vậy tại vị trí mà RAC = 4 (W) hoặc RAC = 8 (W) thì vôn kế chỉ 1 (V) c- Tìm số chỉ vôn kế, khi RAC = 10 (W) Khi RAC = 10(W) => RCB = 18 - 10 = 8 (W) => UAC = IAC . RAC = 0,5 .10 = 5 (V) Suy ra số chỉ của vôn kế là: UV = UAC - U1 = 5 - 3 = 2 (V) Vâỵ khi RAC = 10W thì vôn kế chỉ 2(V) V- Kết qủa nghiên cứu và ứng dụng của đề tài: - Qua thời gian giảng dạy và bồi dưỡng học sinh giỏi, tôi nhận thấy yếu tố quan trọng nhất để nâng cao chất lượng học sinh đó là phương pháp giảng dạy của giáo viên. Trong đó đối với việc dạy bồi dưỡng học sinh giỏi thì một vấn đề đặc biệt quan trọng là giáo viên phải xây dựng được một hệ thống phương pháp giải bài tập cho từng loại bài. Có vậy học sinh mới hiểu và nắm vững một cách tổng quát về kiến thức, trên cơ sở đó các em mới có thể tự học, tự nghiên cứu tài liệu và có hứng thú học tập. Đây là đề tài đã được xây dựng qua quá trình bản thân trực tiếp nghiên cứu và vận dụng trong khi dạy bồi dưỡng học sinh giỏi. Do đó đây là những vấn đề rất thiết thực và có tính ứng dụng cao. Mỗi nội dung trong đề tài mang tính chất khái quát cao và đã được giải quyết một cách cụ thể, chi tiết. Chính vì vậy đây không chỉ đơn thuần là những kiến thức, những phương pháp để áp dụng cho việc giải các bài tập về mạch cầu điện trở và hệ thống các tính chất quan trọng của mạch cầu điện trở. Do đó việc giảng dạy theo nội dung của đề tài này sẽ không chỉ giúp học sinh có một hệ thống phương pháp giải bài tập, mà quan trọng hơn là các em nắm được bản chất vật lý và các mối quan hệ của những đại lượng vật lý (U,I, R) trong mạch cầu điện trở. Mặc dù đây là một chuyên đề rộng và khó, xong qua quá trình vận dụng đề tài này vào thực tế tôi nhận thấy tất cả các học sinh đều tiếp thu nhanh và vận dụng tốt các phương pháp đó vào việc giải các bài tập về mạch cầu. Vi - triển vọng của đề tài: - Bài tập về mạch cầu là một nội dung rất rộng và khó. Bởi lý do các phương pháp để giải loại bài tập này đòi hỏi phải vận dụng một lượng kiến thức tổng hợp và nâng cao. Đối với học sinh lớp 9 thì việc nắm được những bài tập như vậy là rất khó khăn. Tôi nghĩ rằng, để học sinh có thể hiểu một cách sâu sắc và hệ thống về từng loại bài tập thì nhất thiết trong qúa trình giảng dạy giáo viên phải phân loại các dạng bài tập và xây dựng các phương pháp giải cụ thể cho từng loại bài. Đặc biệt đối với các bài tập về mạch cầu, đây không chỉ là nội dung quan trọng trong chuyên đề bồi dưỡng học sinh giỏi Vật lý lớp 9 mà các bài tập này sẽ được tiếp tục nghiên cứu nhiều hơn ở chương trình vật lý lớp 11 và 12. Do đó đây chính là nền tảng vững chắc để các em có thể học tốt môn vật lý ở các lớp trên. - Đề tài này chỉ xây dựng phương pháp giải bài tập cho một mảng nhỏ trong số các dạng bài tập nâng cao của vật lý lớp 9. Tuy nhiên, bằng phương pháp tương tự, trong qúa trình giảng dạy mỗi giáo viên đều có thể xây dựng các phương pháp giải cho tất cả các loại bài tậ còn lại. Đây chính là phương pháp tốt nhất để mỗi giáo viên có thể tự bồi dưỡng chuyên môn cho mình và đây cũng là biện pháp tốt nhất để nâng cao chất lượng dạy học. Vii - kết luận: Việc phân loại và xây dựng các phương pháp giải bài tập Vật lý bao giờ cũng là vấn đề khó khăn nhất đối với tất cả các giáo viên dạy môn Vật lý. Song đây là công việc nhất thiết phải làm thì mới mang lại hiệu quả cao trong quá trình dạy học. - Qua quá trình nghiên cứu và giảng dạy môn vật lý, cùng với sự học hỏi kinh nghiệp từ đồng nghiệp tôi đã mạnh dạn xây dựng đề tài này. Do thời gian có hạn, đề tài này không tránh khỏi những khiếm khuyết cần phải sửa chữa, bổ xung. Rất mong có sự đóng góp ý kiến của các cấp lãnh đạo và của các đồng nghiệp để đề tài của tôi hoàn thiện tốt hơn.
Tài liệu đính kèm:
 phuong phap giai bai toan mach cau.doc
phuong phap giai bai toan mach cau.doc





