Tài liệ Đại số Lớp 11 - Phương pháp giải phương trình lượng giác - Hoàng Văn Sơn
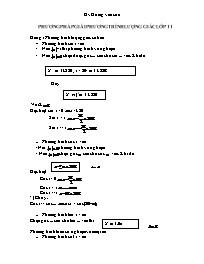
1.1 Phương trình đưa được về phương trình đại số nhờ công thức cơ bản
Bài toán 4.1. (Đại học bách khoa Hà Nội - 1996). Giải phương trình
Lời giải:
Ta áp dụng hằng đẳng thức:
Ta có:
Bởi vậy phương trình đã cho có dạng:
Bài toán 4.2. Giải phương trình.
Lời giải:
Thay bởi 1- sin2x ta được
8(1- sin2x) + 6 sinx -3 = 0
8 sin2x- 6 sinx – 5 =0
Hay
8t2 – 6t -5 = 0 với t = sinx
Phương trình có nghiệm (loại)
a) sin x = =
b) sin x = , phương trình vô nghiệm do sin x
vậy nghiệm của phương trình là:
Bài 4.3: Tìm nghiệm trong khoảng từ (0; ) của phương trình
Lời giải:
Thay bởi ta được
Hay 3t2-4t+1 =0 với t= cot2x= t với t>0
Suy ra t=1 và t=
a) cot2x= 1 suy ra cotx= 1
suy ra x=
b) cot2x = suy ra cotx = suy ra x=
bằng cách biểu diễn các họ nghiệm (1) và (2) trên đường tròn lượng giác ta được nghiệm trong khoảng từ (0, ) là;
PHƯƠNG PHÁP GIẢI PHƯƠNG TRÌNH LƯỢNG GIÁC LỚP 11 Dang1: Phương trinh lượng giác cơ bản Phương trình sinx = m Nếu >1 thì phương trình vô nghiệm Nếu chọn được góc sao cho sin = m. Khi đó X = +k2 ; x= - + k2 X= (-1)k + k2 Hay Với K Đặc biệt: sin x= 0 x= k Sin x = 1 Sin x= -1 Phương trình cos x = m -Nếu phương trình vô nghiệm - Nếu chọn góc sao cho cos = m. Khi đó Đặc biệt: Cosx= 0 Cosx = 1 Cosx =-1 *) Chú ý. Cosx= - cos cosx = cos( Phương trình tan x = m X=+ Chọn góc sao cho tan = m thì Phương trình luôn có nghiệm với mọi m Phương trình cot x = m X= + Nếu là góc sao cho cot= m thì Ví dụ về các dạng toán Có hai phương pháp chung nhất để đưa một phương trình lượng giác nào đó về phương trình lượng giác cơ bản: Đưa phương trình đã cho về dạng phương trình đại số. Đưa phương trình đã cho về dạng tích các phương trình lượng giác cơ bản : Ta sẽ lần lượt nêu các ví dụ minh họa cho từng phương pháp 1.1 Phương trình đưa được về phương trình đại số nhờ công thức cơ bản Bài toán 4.1. (Đại học bách khoa Hà Nội - 1996). Giải phương trình Lời giải: Ta áp dụng hằng đẳng thức: Ta có: Bởi vậy phương trình đã cho có dạng: Bài toán 4.2. Giải phương trình. Lời giải: Thay bởi 1- sin2x ta được 8(1- sin2x) + 6 sinx -3 = 0 8 sin2x- 6 sinx – 5 =0 Hay 8t2 – 6t -5 = 0 với t = sinx Phương trình có nghiệm (loại) sin x == sin x = , phương trình vô nghiệm do sin x vậy nghiệm của phương trình là: Bài 4.3: Tìm nghiệm trong khoảng từ (0;) của phương trình Lời giải: Thay bởi ta được Hay 3t2-4t+1 =0 với t= cot2x= t với t>0 Suy ra t=1 và t= cot2x= 1 suy ra cotx=1 suy ra x= cot2x = suy ra cotx = suy ra x= bằng cách biểu diễn các họ nghiệm (1) và (2) trên đường tròn lượng giác ta được nghiệm trong khoảng từ (0,) là; Bài 4.4 (Đại học bách khoa 1994).Giải phương trình Lời giải: Cosx khi đó phương trình đã cho tương đương với phương trình. (1) Đặt u = cos 2x thay vào phương trình (1) và rút gọn ta được. 2u2+ 3u +1= 0 cos 2x =-1 (loại) cos 2x =-= cos Đáp số : Bài toán 4.5. ( Học viện kĩ thuật quân sự - 1997) Giải phương trình. Lời giải: Phương trình đã cho tương đương với Do cos x = 0 không thỏa mãn phương trình nên ta có thể chia cả hai vế cho cos3x ≠ 0 Phương trình đưa về dạng tích các phương trình cơ bản Bài toán 4.6.( Đề thi đại học – 1980). Giải phương trình Lời giải: Khi đó phương trình đã cho tương đương với: Từ (1) và (2) ta có x= Bài toán 4.7.Giải phương trình Lời giải: Do Nên phương trình đã cho tương đương với Vậy nghiệm của phương trình cho là; Bài toán. 4.8 (Đại học mở chất – 1997).Giải phương trình. Lời giải. Điều kiện sinx . Khi đó phương trình đã cho tương đương với. Do nên Do sinx nên Bởi vậy hệ trên vô nghiệm Bài toán: 4.9.(Đại học ngoại thương - 1996) .Giải phương trình Lời giải: Biến đổi vế trái thành tích ta có: Phương trình này có nhiều cách giải,chẳng hạn thay. Hoặc sử dụng công thức Hoặc có thể giải như sau; Hoặc dùng công thức hạ bậc ta có; Đáp số: Bài 4.10.(Đề thi đại học - 1986). Giải phương trình Lời giải. Trước hết ta xét điều kiện mẫu số khác không. Khi đó phương trình đã cho tưng đương với. Do điều kiện ta chỉ lấy giá trị của x,ứng với m=2k, Đáp số: Bài tập thực hành. Giải phương trình sau bằng cách đưa về phương trình đại số Bài 1. Bài 2. Bài 3. Giải các phương trình sau bằng cách đừa về phương trình tích Bài 4. (Đại học quốc gia khối B - 1997) Bài 5.(Đại học sư phạm - 1991) Bài 6. Bài 7. (Đại học bách khoa- 1993) Bài 8. Bài 9. (Đại học luật - 1996) Một số dạng phương trình thường gặp ở mục trước chúng ta đã xét một số ví dụ minh họa cho hai phương pháp chung nhất đẻ một giải phương trình lượng giác;một là đưa phương trình đã cho về dạng phương trình đại số, hai là đưa về dạng tích các phuong trình lượng giác cơ bản. Những chỉ dẫn tổng quát về các phương pháp đó là không có, mà tuy theo từng bài cụ thể đẻ đưa ra những biến đổi thích hợp. Tuy nhiên chúng ta có thể nêu ra một số phương trình thường gặp và những kĩ năng cơ bản để áp dụng cho những dạng đó 1. Phương trình dạng ( ) Cách giải 1:Đồng thời đưa sinx và cosx về .Khi đó ta được một phương trình bậc hai đối vói t=.Cách này thường sử dụng trong một số bài toán biện luận Cách giải 2: Đưa asinx +bcosx về sin hoặc cosin của góc phụ. Cụ thể chia cả hai vế của phương trình cho Tiếp đó đặt ta được Cũng có thể đặt khi đó ta được Cách giải 3. Nếu ,chia cả hai vế cho a rồi đặt ta được Bài toán 5.1 . Giải phương trình Lời giải: Cách 1: chỉa cả hai vế cho 2 Cách 2; Thay vào phương trình ta được Bài toán 5.2 : (Đại học kinh tế quốc dân - 1997).Tìm nghiệm của phương trình thỏa mãn điều kiện Lời giải: Chia cả hai vế cho 2 ta được Để lấy nghiệm trong khoảng ta xét. Đáp số: Nhận xét: do phép biến đổi đã nêu nên phương trình (1) có nghiệm khi và chỉ khi Bài toán:5.3 với giá trị nào của m thì phương trình sau có nghiệm Điều kiện để phương trình có nghiệm là: 2.Phương trình dạng Cách giải 1. Xét trường hợp cosx =0 bằng cách thay trực tiếp vào phương trình. Với trường hợp cosx ta chia cả hai vế cho cos2x và ta thu được phương trình bậc hai đối với t= tan2x lưu ý rằng: Cách giải 2. Dùng công thức hạ bậc Và công thức 2.sinx.cosx= sin2x để đưa phương trình đã cho về dạng Bài toán:5.4. Giải phương trình lời giải: Cách 1:khi cosx =0 thì sin2x=1, do đó cosx=0 không thỏa mãn phương trình Với cosx ta chia cả hai vế cho : Do tổng các hệ số bằng không nên phương trình đã cho có hai nghiệm Tuy nhiên phương trình phải qua một số phép biến đổi lượng giác mới có thể lấy được nghiệm. Bây giờ ta xét cách giải thứ hai ; Cách 2 : Biến đổi tương đương phương trình đã cho như sau ; Phương trình giải được nhờ công thức cộng cung và các hệ quả của chúng (công thức nhân đôi,công thức hạ bậc) Bài toán 5.5. Giải phương trình sau. Lời giải : Theo công thức hạ bậc ta có : Vậy nghiệm của phương trình đã cho là : Bài toán : 5.6. (Đại học nông nghiệp – 1996 ).Giải phương trình Lời giải : Ta có Bởi vậy phương trình đã cho có dạng Với điều kiện cos2x ta có Do cos2x nên k= 2n+1. Vậy Phương trình giải được nhờ sử dụng công thức biến đổi tổng thành tích và tích thành tổng Bài toán: 5.7 . Tìm nghiệm trong khoảng của phương trình sau. Lời giải: Điều kiện cos2x. Theo công thức biến đổi tổng thành tích ta có. Với 00, do đó Để lấy nghiệm trong khoảng ta xét Từ đó ta thấy k= 0 ,k = 1 và Với ta có sinx<0, do đó Xét điều kiện : ta được k = 2 và k = 3. Do đó Vậy nghiệm của phương trình trong khoảng là ; Bài toán : 5.8 Giải phương trình Lời giải : Khi đó phuingw trình đã cho tương đương với. Do Đáp số : Chú ý :qua một số ví dụ vừa xét ta thấy rằng khi giải phương trình cần phải đặt điều kiện và cần phải kiểm tra lại các điều kiện này đối với các giá trị tìm được đẻ loại bớt nghiệm ngoại lai (nếu có). Phương trình giải được nhờ đưa vào hàm số lượng giác của các góc phụ. Bài toán. 5.9 Giải phương trình Lời giải : Biến đổi phương trình như sau Từ đó suy ra các nghiệm Bài 5.10 (Đại học quốc gia – Khối A – 1997 ). Giải phương trình Lời giải: Ta biến đổi phương trình như sau: Chia cả hai vế cho Vô nghiệm vì sinx Vậy nghiệm của phương trình là x= Phương trình có chứa và Nếu phương trình có chứa các số hạng dạng và thì luôn đặt làm ẩn phụ Bài toán.5.11. Giải phương trình Lời giải: Đặt t= sinx- cosx = khi đó và Bởi phương trình có dạng. Do đó 1- sin2x = 1 Nhận xét : Nếu không sử dụng các biến đổi như trên ta sẽ giải các phương trình và việc lấy nghiệm sẽ dài dòng hơn nhiều Bài toán : 5.12 .Giải phương trình Lời giải : Lưu ý rằng ; phương trình đã cho được viết dưới dạng. đặt ta được Do đó phương trình vô nghiệm Đáp số : Bài 5.12 .Giải phương trình Lời giải : Đặt khi đó Cos2x,sin2x= và Bởi phương trình đã cho có dạng Cả hai giá trị này đều bị loại do Đáp số : 7.Phương pháp đánh giá từng vế Bài toán :5.14. ( Đại học kiến trúc – 1997).Giải phương trình sau. Lời giải : Phương trình đưa được về dạng. Ta cần tìm các số nguyên k và m thỏa mãn hệ trên Phương trình nay vô nghiệm do vế trái lẻ còn vế phải chẫn Vậy phương trình đã cho là vô nghiệm Bài tập thực hành 5 Giải các phương trình sau 1. 2. 3. Giải các phương trình nhờ công thức cộng cung và các hệ quả 4. 5. 6. 7.Tìm nghiệm trong khoảng của phương trình Giải phương trình sau nhờ các công thức liên quan tới tích và tổng 8. 9.(Đại học Quốc gia – khối B- 1995) 10. b) (Đại học – khối A - 1987) Giải phương trình sau nhờ đưa thêm hàm số lượng giác của các góc phụ 11. 12. Giải phương trình sau 13. 14. 15. TỔNG HỢP KĨ NĂNG GIẢI TOÁN Trong tiết này chúng ta xét một số ví dụ ở mức độ khó hơn,đòi hỏi vận dụng tổng hợp những kỹ năng cơ bản đã trình bầy ở mục trước, cũng như vận dụng những kiến thức khác về đại số. 1.Phương trình có chữa điều kiện Đối với một số phương trình,ngay từ đầu hoặc trong quá trình giải ta cần phải tiến hành đặt các điều kiện cần thiết và tới khi lấy được nghiệm cần lưu ý đối chiếu với các điều kiện này để loại bớt nghiệm ngoại lai (nếu có). Bài toán 6.1. Giải các phương trình sau Lời giải: Điều kiện sinx.cosx>0. khi đó bởi vậy phương trình có dạng điều kiện cosx + sinx dẫn tới Cosx>0; sinx>0 Khi đó (1) Do điều kiện sinx> 0; cosx>0 nên ta có là nghiệm của phương trình đã cho Bài toán 6.2. Giải phương trình sau Lới giải: Điều kiện Khi đó phương trình đã cho tương đương với. Ta thấy sinx = -1 loại do điều kiện cosx Các nghiệm này đều thỏa mãn điều kiện sin4x Chú ý: Với cách biến đổi khác ta phải thận trongjkhi lấy nghiệm Chẳng hạn. Thử lại điều kiện sin4x ta có a)(Loại) Bởi vậy k= 3t hoặc k=3t+1. khi đó 2.Một số kĩ năng khác Các phương trình lượng giác khá đa dạng, phong phú về thể loại. Với mỗi bài toán cẩn vận dụng linh hoạt những kĩ năng biến đổi cho phù hợp.Những kĩ năng này thường được hình thành sau qua strinhf giải một loạt bài tập khác nhau Bài toán : 6.3 (ĐH ngoại ngữ - 1992 ). Giải phương trình Lời giải : Phương trình đã cho có thể viết dưới dạng Nếu thì , do đó phương trình không thỏa mãn. Bởi vậy chia cả hai vế cho ta được Đặt t=tanx, thay vào phương trình (1) ta được Phương trình 3t2+ 3t + 1= 0 vô nghiệm do đó Bài 6.4 (Đại học ngoại thương – 1994 ).Giải phương trình sau. Lời giải : Phương trình đã cho được biến đổi như sau : Từ đó ta suy ra : Xét từng trường hợp : sin6x = 0. khi đó từ (2) ta suy ra Giá trị này thỏa mãn sin6x= 0 khi đó sin2 6x = 1 và từ (2) ta suy ra Cả hai giá trị này đều thỏa mãn cos6x = 0 Đáp số: Bài 6.5 Tìm các nghiệm trong khoảng của phương trình sau Lời giải: Phương trình đã cho tương đương với hệ Từ đó Trong khoảng ta nhận được các giá trị Khi thử vào điều kiện (2) trong số 4 giá trị trên ta nhận được hai giá trị thỏa mãn là; Bài toán:6.6 Giải phương trình sau. Cos3x – cos2x = sin3x. Lời giải: Áp dụng công thức góc nhân ba ta có. Cos3x- sin3x =(4 cos3x – 3cosx)- (3sinx – 4 sin3x) = 4(cos3x + sin3x) – 3(sinx + cosx) =(sinx + cosx)(1 – 4 sin x.cosx) Cos2x= cos2x – sin2x =(cosx - sinx) (cosx+ sinx) Bởi vậy phương trình tương đương với. (cosx+ sinx) Đặt khi đó bởi vậy ta có phương trình Từ đó suy ra: Vậy phương trình đã cho có các nghiệm Bài toán. 6.7. (ĐH bách khoa – 1997 ).Giải phương trình lượng giác Lời giải: Điều kiện khi đó ta có Đối chiếu với điều kiện ta lấy. Từ phương trình (1) suy ra cosx= 0 hoặc cosx = 1,cả hai giá trị này không thỏa mãn phương trình (2). Vậy hệ vô nghiệm Đáp số: Bài toán.6.8. Giải phương trình lượng giác sau Lời giải: Điều kiện sinx , khi đó ta có. Đặt khi đó Phương trình (1) trở thành Loại Từ đó. 3.Biện luận phương trình có chứa tham số Bài toán 6.9. Cho phương trình Giải phương trình khi m= 1 Tìm m để phương trình có nghiệm thỏa mãn Lời giải. Phương trình có dạng Khi m= 1 ta có. Phương trình có nghiệm trong khoảng khi và chỉ khi tính nghiệm của f(t) ta được Từ đó suy ra Bài toán : 6.10 (Đề thi ĐH học – 1979 ) Giải phương trình Xác định a để phương trình Tương đương với phương trình (1) Lời giải: a)Áp dụng công thức biến đổi tích thành tổng ta được Ta cũng biến đổi sin5x= sin(2x + 3x) Đặt y = cos2x thì (2) có dạng Với thì : Nếu y = 1 là nghiệm của phương trình (3) thì Khi đó (3) trở thành 4y3 – 2ay2+ (a- 3)y+a- 1=0 Tổng các hệ số của nghiệm này bằng 0 nên y = 1 là nghiệm của phương trình. Chia cho (y –1) Ta được Vậy phương trình (2) tương đương với phương trình (1) hoặc bị loại. Bởi vậy sẩy ra các trường hợp sau Đáp số : a=0 ; a<- 1 Bài toán 6.11 .Chứng mình rằng phương trình sau luôn có nghiệm vơi mọi m Lời giải : Điều kiện sinx khi đó phương trình (1) tương đương với Sinx – cosx = m sinx.cosx (2) Đặt t = sinx – cosx = ta được và t2 = 1 – 2sinx.cosx Bởi vậy phương trình (2) trở thành (3) Bài toán trở thành : Chứng tỏ rằng phương trình (3) luôn có nghiệm với mọi . Thật vậy. Nếu m = 0 thì f(t) = 2t = 0 suy ra t = 0 Nếu m thì f(1).f(-1) = -4 <0 Điều này chứng tỏ phương trình luôn có nghiệm Bài tập thực hành 6 Giải các phương trình 1. 2.(ĐH dân lập phương đông – 1996 ) Sin4x + (1- sinx )4 = 17 3.Tìm nghiệm trong khoảng của phương trình 4.Chứng minh phương trình sau vô nghiệm Giải các phương trình sau 5. 6.(ĐH ngoại thương – 1995 ) 4cosx - 2cos2x - cos4x = 1 7. 8.(ĐH năm 1982) 9.Tìm nghiệm của các phương trình sau Thỏa mãn hệ Giải các phương trình sau 10. 11.(ĐH mỏ địa chất – 1993 ) 12.(ĐH bách khoa – 1992 ) 13. Vơi giá trị nào cưa m thì phương trình sau có nghiệm 14.Tìm mọi giá trị của a đẻ phương trình sau có nghiệm Bài toán tìn giá trị lớn nhất và nhở nhất của một hàm số lượng giác 1.(ĐH – 1982 ). Tìm giá trị lớn nhất và bé nhất của tổng các bình phương các nghiệm của phương trình bậc hai Lời giải : Phương trình đã cho luôn có nghiệm vì có. Theo định lí Vi- ét ta có. Với . Bởi vậy tổng S có giá trị lớn nhất bằng 13+5=18, Giá trị nhở nhất 13-5=8 2.(ĐH kiến trúc – 1996 ).Tìm giá trị lớn nhất của hàm số Lời giải : Giả sử y0 là một giá trị của hàm số. Thế thì phương trình sau có nghiệm Phương trình sau cùng có dạng bậc nhất đối với sinx và cosx. Nó có nghiệm khi và chỉ khi Vậy y0 là giá trị lớn nhất của hàm số điều này xẩy ra khi 3.Tìm giá trị lớn nhất và nhỏ nhất của biểu thức P= sin2x+sin4y+sin6z khi sinx + siny +sinz =0 Dễ thấy Pmin = 0 khi sinx = siny = sin z =0 Nhận xét rằng trong ba số sinx,siny,sinz phải có hai số cùng dấu,chẳng hạn sinx và siny. Khi đó P=sin2x+sin4y+sin6z Ta chỉ ra những giá trị của x,y,z để xảy ra P =2. Đó là khi Vậy Pmax = 2 3. Giải phương trình Lời giải : Điều kiện Phương trình đã cho có thể viết được dưới dạng Giá trị này thỏa mãn cos2x Bình phương cả hai vế và ước lược ta được Giá trị này thỏa mãn điều kiện sinx – cosx Đáp số :
Tài liệu đính kèm:
 Phương pháp giải phương trình lượng giác lớp 11.doc
Phương pháp giải phương trình lượng giác lớp 11.doc





