Giáo án tự chọn môn Toán Lớp 7 - Tuần 23, Tiết 2: Luyện tập (tiếp theo) - Năm học 2009-2010 - Phạm Thị Kim Quyên
A. Mục tiêu:
- Phát huy khả năng làm toán cm của HS.
- Củng cố các trường hợp bằng nhau của tam giác( 3 trường hợp)
- Rèn luyện kĩ năng các trường hợp bằng nhau cua 2 tam giác
- Rèn luyện kĩ năng vẽ hình và chứng minh.
B. Chuẩn bị:
Bảng phụ,bài tập
C. Tiến trình bài dạy:
TG HỌAT ĐỘNG CỦA GV HỌAT ĐỘNG CỦA HS GHI BẢNG
40
Hoạt động 1: Luyện tập
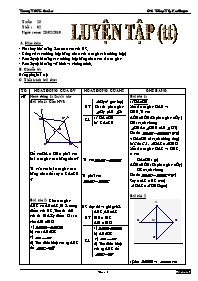
Bài tập 1: Cho HVẽ
Để cm OA = OB ta phải cm hai tam giác nào bằng nhau?
Ta cần cm hai tam giác nào bằng nhau để suy ra CA=CB ?
Bài tập 2: Cho tam giác ABC có AB=AC ,M là trung điểm của BC,Trên tia đối của tia MA lấy điểm D sao cho AM =MD
a)
b) cm : AB//DC
c)
d) Tìm điều kiện cua tg ABC để
và có những yếu tố nào bằng nhau?
Vậy 2 tam giác bằng nhau theo những trường hợp nào? Hãy cm?
Để cm AB // DC ta phải cm ntn?
Cm cm ntn?
khi nào?
có liên quan gì tới góc BAC của tam giác ABC?
Vậy khi có điều kiện gì ?
GT
xOy(# góc bẹt)
Ot : tia phân giác
xOy ;ABOt
KL
a/ OA =OB
b/ CA=CB
Ta cm
Ta phải cm
HS đọc đề và ghi gt-kl
GT
ABC, AB=AC
MB = MC
AM = MD
KL
a)
b) AB//DC
c)
d) Tìm điều kiện của tg ABC để
1 HS chứng minh
AM = MD(gt)
MB =MC(gt)
(đđ)
Cm:( slt)
HS lên bảng trình bày
khi
Mà khi
ĐK: AB =AC, Bài tập 1:
a/ OA=OB
Xét 2 tam giác OAH và OBH,Ta có:
AÔH=BÔH(Ot phân giác xÔy )
OH: cạnh chung
OHA=OHB (AB OT)
Do đó ( gcg)
->OA=OB (2 cạnh tương ứng)
b/ CA=CB , OAC=OBD
Xét 2 tam giác OAC và OBC, ta có:
OA=OB ( gt)
AÔH=BÔH( Ot phân giác xÔy)
OC :cạnh chung
Do đó (cgc)
Suy ra:AC = BC (ctu)
OAC= OBD(gtu)
Bài tập 2
a)Xét và có:
AM = MD(gt)
MB =MC(gt)
(đđ)
Vậy =(cgc)
b) =(cmt)
(gtu)
Mà 2 góc này ở vị trí so le trong nên: AB//DC
c) Ta có :(ccc)
vì AB = AC(gt)
AM cạnh chung
(gtu)
(kb)
Hay
d) Ta có:
khi
Vì:(cmt)
Mà khi
Vì:
Do
Vậy khi tam giác ABC có AB =AC và
Tuần: 23 Tiết : 02 Ngày soạn: 28/02/2010 A. Mục tiêu: - Phát huy khả năng làm toán cm của HS. - Củng cố các trường hợp bằng nhau của tam giác( 3 trường hợp) - Rèn luyện kĩ năng các trường hợp bằng nhau cua 2 tam giác - Rèn luyện kĩ năng vẽ hình và chứng minh. B. Chuẩn bị: Bảng phụ,bài tập C. Tiến trình bài dạy: TG HỌAT ĐỘNG CỦA GV HỌAT ĐỘNG CỦA HS GHI BẢNG 40’ Hoạt động 1: Luyện tập Bài tập 1: Cho HVẽ Để cm OA = OB ta phải cm hai tam giác nào bằng nhau? Ta cần cm hai tam giác nào bằng nhau để suy ra CA=CB ? Bài tập 2: Cho tam giác ABC có AB=AC ,M là trung điểm của BC,Trên tia đối của tia MA lấy điểm D sao cho AM =MD a) b) cm : AB//DC c) d) Tìm điều kiện cua tg ABC để và có những yếu tố nào bằng nhau? Vậy 2 tam giác bằng nhau theo những trường hợp nào? Hãy cm? Để cm AB // DC ta phải cm ntn? Cm cm ntn? khi nào? có liên quan gì tới góc BAC của tam giác ABC? Vậy khi có điều kiện gì ? GT xOy(# góc bẹt) Ot : tia phân giác xOy ;ABOt KL a/ OA =OB b/ CA=CB Ta cm Ta phải cm HS đọc đề và ghi gt-kl GT ABC, AB=AC MB = MC AM = MD KL a) b) AB//DC c) d) Tìm điều kiện của tg ABC để 1 HS chứng minh AM = MD(gt) MB =MC(gt) (đđ) Cm:( slt) HS lên bảng trình bày khi Mà khi ĐK: AB =AC, Bài tập 1: a/ OA=OB Xét 2 tam giác OAH và OBH,Ta có: AÔH=BÔH(Ot phân giác xÔy ) OH: cạnh chung OHA=OHB (AB OT) Do đó ( gcg) ->OA=OB (2 cạnh tương ứng) b/ CA=CB , OAC=OBD Xét 2 tam giác OAC và OBC, ta có: OA=OB ( gt) AÔH=BÔH( Ot phân giác xÔy) OC :cạnh chung Do đó (cgc) Suy ra:AC = BC (ctu) OAC= OBD(gtu) Bài tập 2 a)Xét và có: AM = MD(gt) MB =MC(gt) (đđ) Vậy =(cgc) b) =(cmt) (gtu) Mà 2 góc này ở vị trí so le trong nên: AB//DC c) Ta có :(ccc) vì AB = AC(gt) AM cạnh chung (gtu) (kb) Hay d) Ta có: khi Vì:(cmt) Mà khi Vì: Do Vậy khi tam giác ABC có AB =AC và 5’ Họat động 2: Hướng dẫn về nhà -Ôn tập phần thống kê mô tả để tiết sau luyện tập đại - Xem lại các phần đã học về các trường hợp bằng nhau của 2 tam giác.
Tài liệu đính kèm:
 tuan 24 tiet 2.doc
tuan 24 tiet 2.doc





