Giáo án môn Hình học Lớp 7 - Tiết 44 đến 45: Ôn tập chương II (tiết 1)
A. TIẾN TRÌNH DẠY HỌC:
GIÁO VIÊN HỌC SINH
Hoạt động 1: ôn tập lại các đn, đl đã học trong chương
Giáo viên nêu câu hỏi 1, 2, 3 trong phần ôn tập của sgk và yêu cầu hs trả lời
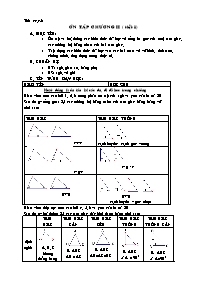
Sau đó gv tổng quát lại các trường hợ bằng nahu của tam giác bằng bảng vẽ như sau:
TAM GIÁC
TAM GIÁC VUÔNG
c-c-c
cạnh huyền- cạnh góc vuông
c- g-c
c- g - c
g-c-g
g-c-g cạnh huyền – góc nhọn
Giáo viên tiếp tục nêu câu hỏi 4, 5, 6 và yêu cầu hs trả lời
Sau đó gv hệ thống lại các tam giác đặc biệt dạng bảng như sau:
TAM GIÁC TAM GIÁC CÂN TAM GIÁC ĐỀU TAM GIÁC VUÔNG TAM GIÁC VUÔNG CÂN
định nghĩa
A, B, C không thẳng hàng
ABC
AB = AC
ABC
AB=AC=BC
ABC
A = 900
ABC
A=900
AB = AC
Yêu cầu hs làm bài 67 SGK
Điền dấu x vào chỗ trống thích hợp:
Câu Đúng Sai
1. trong 1 tam giác góc nhỏ nhất là góc nhọn
2. Trong 1 tg có ít nhất 2 hai góc nhọn
3. Trong một tam giác , góc lớn nhất là góc tù
4. Trong một tam giác vuông hai góc nhọn bù nhau
5. Nếu A là góc ở đáy của tam giác cân thì A< 900="">
6. Nếu A là góc ở đỉnh của một tam giác cân thì A< 900="">
X
X
X
X
X
Tiết 44,45: ÔN TẬP CHƯƠNG II ( tiết 1) MỤC TIÊU: Ôn tập và hệ thống các kiến thức đã học về tổng ba góc của một tam giác, các trường hợ bằng nhau của hai tam giác. Vận dụng các kiến thức đã học vào các bài toán về vẽ hình, tính táon, chứng minh, ứng dụng trong thực tế. CHUẨN BỊ: GV: sgk, giáo án, bảng phụ HS: sgk, vở ghi TIẾN TRÌNH DẠY HỌC: GIÁO VIÊN HỌC SINH Hoạt động 1: ôn tập lại các đn, đl đã học trong chương Giáo viên nêu câu hỏi 1, 2, 3 trong phần ôn tập của sgk và yêu cầu hs trả lời Sau đó gv tổng quát lại các trường hợ bằng nahu của tam giác bằng bảng vẽ như sau: TAM GIÁC TAM GIÁC VUÔNG c-c-c cạnh huyền- cạnh góc vuông c- g-c c- g - c g-c-g g-c-g cạnh huyền – góc nhọn Giáo viên tiếp tục nêu câu hỏi 4, 5, 6 và yêu cầu hs trả lời Sau đó gv hệ thống lại các tam giác đặc biệt dạng bảng như sau: TAM GIÁC TAM GIÁC CÂN TAM GIÁC ĐỀU TAM GIÁC VUÔNG TAM GIÁC VUÔNG CÂN định nghĩa A, B, C không thẳng hàng r ABC AB = AC r ABC AB=AC=BC r ABC Ð A = 900 r ABC Ð A=900 AB = AC Yêu cầu hs làm bài 67 SGK Điền dấu x vào chỗ trống thích hợp: Câu Đúng Sai trong 1 tam giác góc nhỏ nhất là góc nhọn Trong 1 tg có ít nhất 2 hai góc nhọn Trong một tam giác , góc lớn nhất là góc tù Trong một tam giác vuông hai góc nhọn bù nhau Nếu Ð A là góc ở đáy của tam giác cân thì Ð A< 900 Nếu Ð A là góc ở đỉnh của một tam giác cân thì Ð A< 900 X X X X X X Yêu cầu hs làm bài 68: Các tính chất sau đây được suy ra từ đl nào? góc ngoài của một tam giác bằng tổng hai góc trong không kề với nó. Trong một tam giác vuông hai góc nhọn pụ nhau. Trong một tam giác đều, các góc bằng nhau. Nếu một tam giác có ba góc bằng nhau thì tam giác đó là tam giác đều. cho hs làm bài tập 107/11 SBT Tìm các ta giác cân trên hình: 360 360 360 Bài 108 /111 sbt Gv đưa đề bài và hình vẽ lên màn hình Gv yêucầu hs hoạt độngtheo nhóm giáo viên nhận xét bài làm của các nhóm giáo viên đưa đề bài 105/111 sbt lên bảng giáo viên hỏi thêm: r ABC có phải là ta giác vuông không? Bài tập : xét xem các mễnh đề sau đúng hay sai ( gv đưa đề lên màn hình và yêu cầu hs hoạt động nhóm) một tam giác cóhaigóc bằng 600 thì đó là tam giác đều. Nếu một cạnh vàhai gó của ta giác này bằng một cạnh và hai góc của tam giác kia thì hai tam giác đó bằng nhau. góc ngoài của mỗi tam giác bao giờ cũng lớn hơn mỗi góc của ta giác đó. nếu mộttam giác có 2 góc bằng 450 tì tam giác đó là tam giác vuông. nếu hai cạnh và một gó của tamgiác này bằng hai cạnh và một góc của tam giác kia thì hai tam giác đó bằng nhau. Hoạt động 3: hướng dẫn về nhà Oân tập lí thuyết và làm các bài tập ôn chương . tiết sau kiễm tramột tiết Đl tổng ba góc trong một tam giác Đl tổng ba góc trong một tam giác ĐL về tam giác cân ĐL về tam giác cân 107/111: r ABC cân vì có AB=AC Ð B1=Ð C1= 1800-360:2=720 r BAD cân vì: Ð A1= Ð B1-Ð D= 720-360= 360=Ð D Tương tự r CAE cân vì Ð A3=Ð E=360 r ADC cân vì có các góc ở đáy bằng 720. r ADE cân vì có Ð D= Ð E= 360 bài 108 tóm tắt cách làm: chứng minh r AOC = r OCB (c-g-c) Ð D=Ð B và Ð A1=Ð C1 Ð A2=Ð C2 Chứng minh: r KAB= r KCD (g-c-g) KA=KC chứng minh: r KOA=r KOC (c-c-c) Ð O1 = Ð O2 do đó OK là phân giác Ð xOy đại diện mộtnhóm trình bày lên bảng. Bài 105: Hs nêu cách tính: Xét tg vuông AEC có: EC2=AC2 – AE2 (đl pitago) EC2=52-42 EC= 3 Có BE =BC- EC=9-3=6 Xét tg vuông ABC có : AB2= BE2+ AE2 ( đl pitago) AB2= 62+42 AB=7,2 hs trả lời: r ABC có: AB2+AC2 =52=25=57 BC2= 92 =81 => AB2+AC2 = BC2 =.> r ABC không phải là tam giác vuông đúng sai sai đúng sai Rút kinh nghiệm:..........................................................................................................
Tài liệu đính kèm:
 Tiet 44,45.doc
Tiet 44,45.doc





