Giáo án Hình học Lớp 7 - Tiết 66: Ôn tập chương III (tiếp theo) - Năm học 2008-2009 - Nguyễn Hữu Thảo
A) Mục tiêu:
- HS củng cố khái niệm và tính chất các loại đường trong tam giác.
- Vận dụng giải bài tập.
B) Chuẩn bị:
Giáo viên: Bảng phụ, thước.
Học sinh: Bảng phụ, thước+ câu 4, 5, 6, 7, 8/86, 87/SGK.
C) Tiến trình dạy học:
1) Ổn định lớp (1):
2) Kiểm tra bài củ (10):
HS1 làm câu hỏi 4, 5/86/SGK.
HS2 trả lời câu hỏi 6/87/SGK:
3) On tập (23):
Hoạt động của thầy Hoạt động của trò Ghi bảng
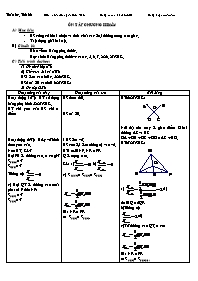
Hoạt động 1(7): GV sử dụng bảng phụ hình 58/87/SGK.
GV chỉ yêu cầu HS chỉ ra điểm
Hoạt động 2(9): HÃy vẽ hình theo yêu cầu.
Nêu GT, KL?
Gọi PH là đường cao, ta có gì?
SPRM = ?
SQPR = ?
Tương tự:
c) Gọi QT là đường cao xuất phát từ P đến NP:
SNRQ = ?
SPRQ = ?
Hoạt động 3(7):
M cách đều hai cạnh góc xOy => M thuộc đâu?
M cách đều hai điểm A, B => M nằm ở đâu?
Vậy M như thế nào?
HS theo dõi.
HS trả lời.
1 HS lên vẽ.
HS còn lại làm tương tự vào vở.
GT: MNP, NR = PR
Q là trọng tâm.
KL: a); b)
c) SMNQ = SNRQ = SPRQ.
Mà NR = PR
=> SNRQ = SPRQ .
M thuộc đường phân giác Oz của góc xOy.
M thuộc đường trung trực AB.
BT66/87/SGK:
Nơi đặt nhà máy là giao điểm O hai đường AC và BC
OA + OB + OC + OD = AC + BD.
BT67/87/SGK:
a) (1)
do MQ = 2QR
b)Tương tự:
(2)
c)Vẽ đường cao QT, ta có:
Mà NR = PR
=>SNRQ = SPRQ (3)
Từ (1), (2), (3) => SMNQ = SNRQ = SPRQ
BT68/88/SGK:
M cách đều hai cạnh goác xOy => M thuộc đường phân giác của góc xOy.
M cách đều hai điểm A, B => M thuộc đương ftrung trực của AB.
Vậy M là giao điểm đường phân giác góc xOy và đường trung trực của AB.
ÔN TẬP CHƯƠNG III (tiếp) Mục tiêu: HS củng cố khái niệm và tính chất các loại đường trong tam giác. Vận dụng giải bài tập. Chuẩn bị: Giáo viên: Bảng phụ, thước. Học sinh: Bảng phụ, thước+ câu 4, 5, 6, 7, 8/86, 87/SGK. Tiến trình dạy học: 1) Ổn định lớp (1’): 2) Kiểm tra bài củ (10’): HS1 làm câu hỏi 4, 5/86/SGK. HS2 trả lời câu hỏi 6/87/SGK: 3) Oân tập (23’): Hoạt động của thầy Hoạt động của trò Ghi bảng Hoạt động 1(7’): GV sử dụng bảng phụ hình 58/87/SGK. GV chỉ yêu cầu HS chỉ ra điểm Hoạt động 2(9’): HÃy vẽ hình theo yêu cầu. Nêu GT, KL? Gọi PH là đường cao, ta có gì? SPRM = ? SQPR = ? Tương tự: c) Gọi QT là đường cao xuất phát từ P đến NP: S NRQ = ? SPRQ = ? Hoạt động 3(7’): M cách đều hai cạnh góc xOy => M thuộc đâu? M cách đều hai điểm A, B => M nằm ở đâu? Vậy M như thế nào? HS theo dõi. HS trả lời. 1 HS lên vẽ. HS còn lại làm tương tự vào vở. GT: êMNP, NR = PR Q là trọng tâm. KL: a); b) c) SMNQ = SNRQ = SPRQ. Mà NR = PR => SNRQ = SPRQ . M thuộc đường phân giác Oz của góc xOy. M thuộc đường trung trực AB. BT66/87/SGK: Nơi đặt nhà máy là giao điểm O hai đường AC và BC OA + OB + OC + OD = AC + BD. BT67/87/SGK: a) (1) do MQ = 2QR b)Tương tự: (2) c)Vẽ đường cao QT, ta có: Mà NR = PR =>SNRQ = SPRQ (3) Từ (1), (2), (3) => SMNQ = SNRQ = SPRQ BT68/88/SGK: M cách đều hai cạnh goác xOy => M thuộc đường phân giác của góc xOy. M cách đều hai điểm A, B => M thuộc đương ftrung trực của AB. Vậy M là giao điểm đường phân giác góc xOy và đường trung trực của AB. 4) Củng cố (8’): - Cách xác định trọng tâm, trực tâm, điểm cách đều 3 cạnh , điểm cách đều 3 đỉnh? BT69/88/SGK: Ta có: O là giao điểm của a, b. êOQS có hai đường cao cắt nhau tại M => M là trực tâm => OM vuông QS. 5) Dặn dò (3’): Học bài+xem BT giải. BTVN: BT70/88/SGK. Chuẩn bị kiểm tra 1 tiết. *) Hướng dẫn bài tập về nhà: BT70/88/SGK: a)M d => MA = MB NB = NM + MB = NM + MA b)Tương tự: Nếu N’ PB => N’B < N’A c) Nếu L d => LA = LB Nếu L BP thì LA > LB Vậy để LA < LB thì L PA.
Tài liệu đính kèm:
 T66.doc
T66.doc





