Giáo án Đại số Lớp 9 - Tiết 59: Kiểm tra 1 tiết - Năm học 2005-2006
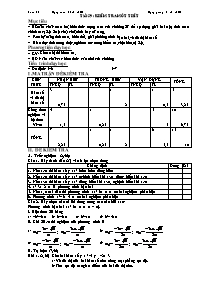
TỔNG 7
2,25 1
0,25 1
2 6
5,5 15
10
II. ĐỀ KIỂM TRA
A. Trắc nghiệm (2,5đ):
Câu 1. Hãy đánh dấu (X) vào ô lựa chọn đúng
Khẳng định Đúng Sai
1. Nếu a>0 thì hàm số y=ax2 luôn luôn đồng biến
2. Nếu a>0 thì hàm số y=ax2 nghịch biến khi x<0, đồng="" biến="" khi="" x="">0
3. Nếu a<0 thì="" hàm="" số="" y="ax2" đồng="" biến="" khi=""><0, nghịch="" biến="" khi="" x="">0
4. x3+3x+2=0 là phương trình bậc hai
5. Nếu a, c trái dấu thì phương trình ax2+bx+c=0 có hai nghiệm phân biệt
6. Phương trình x2–5x+4=0 có hai nghiệm phân biệt
Câu 2. Hãy chọn câu trả lời đúng trong các câu hỏi sau:
Phương trình bậc hai ax2+bx+c=0 (a 0).
I. Biệt thức bằng
a/ –b2–4ac b/ b–4ac c/ b2–ac d/ b2–4ac
II. Khi >0 thì nghiệm của phương trình là
a/ b/
c/ d/
B. Tự luận (7,5đ)
Bài 1. (2,5đ) Cho hai hàm số y=x2 và y= –2x+3
a/ Vẽ đồ thị của hai hàm số trên cùng mặt phẳng tọa độ.
b/ Tìm tọa độ các giao điểm của hai đồ thị trên.
Bài 2.(3đ) Giải phương trình
a/ x2–4x=0
b/ x2–5x+6=0
c/ (2– )x2–(2+ )x+2 =0
Bài 3. (2đ) Cho phương trình x2–2(m+1)x+m2+1=0
a/ Giải phương trình khi m=2
b/ Tìm m để phương trình trên:
+/ Vô nghiệm
+/ Có nghiệm
Tuần:30 Ngày soạn: 02/04/2006 Ngày giảng: 04/04/2006 Tieát 59 : KIEÅM TRA MOÄT TIEÁT Mục tiêu – HSnaém chaéc toaøn boä kieán thöùc troïng taâm cuûa chöông IV ñeå aùp duïng giaûi baøi taäp; tính toaùn chính xaùc; laäp luaän chaët cheõ,trình baøy roõ raøng. – Reøn kyõ naêng tính toaùn, bieán ñoåi, giaûi phöông trình bậc hai, vẽ đồ thị hàm số – Giaùo duïc tính trung thöïc,nghieâm tuùc trong kieåm tra,chòu khoù,töï laäp. Phương tiện dạy học: – GV: Chuaån bò ñeà kieåm tra. – HS: Naém chaéc caùc kieân thöùc caàn nhôù cuûa chöông Tiến trình dạy học: – Ổn định: 9/6 9/7 I .MA TRẬN ĐỀ KIỂM TRA KIẾN THỨC NHẬN BIẾT THÔNG HIỂU VẬN DỤNG TỔNG TNKQ TL TNKQ TL TNKQ TL Hàm số và đồ thị hàm số 3 0,75 1 2 1 0,5 5 3,25 Công thức nghiệm và hệ thức Vi–ét 4 1,5 1 0,25 5 5 10 6,75 TỔNG 7 2,25 1 0,25 1 2 6 5,5 15 10 II. ĐỀ KIỂM TRA A. Trắc nghiệm (2,5đ): Câu 1. Hãy đánh dấu (X) vào ô lựa chọn đúng Khẳng định Đúng Sai 1. Nếu a>0 thì hàm số y=ax2 luôn luôn đồng biến 2. Nếu a>0 thì hàm số y=ax2 nghịch biến khi x0 3. Nếu a0 4. x3+3x+2=0 là phương trình bậc hai 5. Nếu a, c trái dấu thì phương trình ax2+bx+c=0 có hai nghiệm phân biệt 6. Phương trình x2–5x+4=0 có hai nghiệm phân biệt Câu 2. Hãy chọn câu trả lời đúng trong các câu hỏi sau: Phương trình bậc hai ax2+bx+c=0 (a0). I. Biệt thức bằng a/ –b2–4ac b/ b–4ac c/ b2–ac d/ b2–4ac II. Khi >0 thì nghiệm của phương trình là a/ b/ c/ d/ B. Tự luận (7,5đ) Bài 1. (2,5đ) Cho hai hàm số y=x2 và y= –2x+3 a/ Vẽ đồ thị của hai hàm số trên cùng mặt phẳng tọa độ. b/ Tìm tọa độ các giao điểm của hai đồ thị trên. Bài 2.(3đ) Giải phương trình a/ x2–4x=0 b/ x2–5x+6=0 c/ (2–)x2–(2+)x+2=0 Bài 3. (2đ) Cho phương trình x2–2(m+1)x+m2+1=0 a/ Giải phương trình khi m=2 b/ Tìm m để phương trình trên: +/ Vô nghiệm +/ Có nghiệm III ĐÁP ÁN A. Trắc nghiệm Mỗi câu trả lời đúng được 0,5đ Câu1/ (0,25 điểm mỗi câu trả lời đúng) S Đ Đ S Đ Đ Câu 2/(0,5 điểm mỗi câu trả lời đúng) d b B. Tự luận Bài 1. (2,5đ). + Lập bảng đối với đồ thị bậc hai 0,5đ + Tìm được hai điểm đối với đồ thị bậc nhất 0,5đ + Vẽ đồ thị y=x2 0,5đ + Vẽ đồ thị y= –2x+3 0,5đ + Tìm được tọa đọ hai giao điểm 0,5đ Bài 2:(3đ) a/ Biến đổi về thành phương trình tích 0,5đ + Tính được hai nghiệm 0,5đ b, c/ Tìm được hệ số 0,25đ + Tính được hoặc sử dụng hệ thức Vi–ét 0,25đ + Tính được chính xác hai nghiệm 0,5đ Bài 3:(2đ) a/ Thay m=2 và giải phương trình 1đ b/ Tính được 0,5đ + Tìm được m để phương trình vô nghiệm 0,25đ + Tìm được m để phương trình có nghiệm 0,25đ IV THỐNG KÊ LỚP GIỎI KHÁ TB YẾU KÉM 9/6 9/7
Tài liệu đính kèm:
 t59.doc
t59.doc





