Nội dung ôn tập chương I môn Hình học Lớp 8

 HÌNH
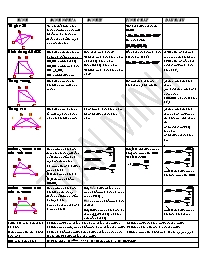
 ĐỊNH NGHĨA
 ĐỊNH LÝ
TÍNH CHẤT
 DẤU HIỆU
Tứ giác lồi
Tứ giác lồi là tứ giác luôn nằm trong nửa mặt phẳng có bờ là đường thẳng chứa bất kỳ cạnh nào của tứ giác
* Có hai đường chéo là AC;DB
*
Các góc đối là:
Hình thang AB//DC
Hình thang là tứ giác có hai cạnh đối song song
AB,DC gọi là hai đáy
AD,BC gọi là cạnh bên
AH _|_D C, 
AH gọi là đường cao
Nếu : hai cạnh bên //
Thì: hai cạnh bên bằng nhau và hai đáy bằng nhau
Nếu: Hai đáy bằng nhau
Thì: Hai cạnh bên bằng nhau và //
Tổng hai góc kề cạnh bên thì bù nhau (1800)
a) Tứ giác có hai cạnh song song là hình thang
b) Tứ giác có tổng hai góc kề một cạnh bên bằng 1800.
Thang vuông.
Hình thang vuông là hình thang có một góc vuông
Có mọi tính chất của hình thang,hình tứ giác
. chứng minh là hình thang
.sau đó chứng minh có 1 góc vuông
( AB//DC và góc D bằng 900.)
Thang cân
Hình thang có hai góc kề một cạnh đáy bằng nhau là hình thang cân
1) có 2 cạnh bên bằng nhau
2) có 2 đường chéo bằng nhau
. chứng minh là hình thang và có một trong các điều sau là h thang cân
có 2góc kề một đáy bằng nhau
- có 2 đường chéo bằng nhau
.
ĐƯỜNG TRUNG BÌNH CỦA TAM GIÁC
Đường trung bình của tam giác là đoạn thẳng nối 2 trung điểm hai cạnh của tam giác
( 1 tam giác có 3 đường trung bình )
MN là đ trung bình ĩ M,N là trung điểm AC;AB.
Đl2. MN là đường trung bình của tam giác ABC 
Thì MN / / BC 
 và
=> MN là đường trung bình của tam giác ABC
ĐƯỜNG TRUNG BÌNH CỦA H- THANG
Đường trung bình của hình thang là đoạn thẳng nối 2 trung điểm hai cạnh bên 
( trong h- thang chỉ có 1 đ trung bình )
Đl1. Nếu đường thẳng qua trung điểm cạnh bên và song song với đáy .
Thì qua trung điểm cạnh bên thứ hai
Đl2. Đường trung bình của h- thang thì // hai đáy và bằng nửa tổng hai đáy
=> MN là đường trung bình của hình thang 
1/Các bài toán dựng hình đã biết
(dựng tam giác cần biết 3 yêu tố.)
1) Dựng một đoạn thẳng bằng đoạn thẳng cho trước ; 2) Dựng một góc bằng một góc cho trước
3) Dựng trung trực, trung điểm của đoạn thẳng cho trước 4) Dựng phân giác của 1 góc cho trước
5) Qua 1 điểm cho trước dựng đường thẳng vuông góc 6) Dựng tam giác biết 3 cạnh (hoặc c,g,c; g,c,g )
(hoặc //) với đường thẳng cho trước
Giải toán dựng hình.
B1.Phân tích: B2. Cách dựng ; B3. Chứng minh ; B4. Biện luận
HÌNH
ĐỊNH NGHĨA
HÌNH
ĐỊNH NGHĨA
CHỨNG MINH:
ĐỐI XỨNG TRỤC
Hình thang cân có 1 trục dối xứng
ĐN1:Hai điểm gọi là đối xứng nhau qua đường thẳng d nếu d là trung trực của đoạn thẳng nối hai điểm đó
ĐN2.Hai hình đối xứng nhau qua đường thẳng nếu:
Mỗi điểm thuộc hình này đối xứng với 1 điểm thuộc hình kia qua đường thẳng d và ngược lại
ĐN3.Đường thẳng d gọi là trục đối xứng của hìnhH nếu: Diểm đối xứng với mỗi điểm thuộc hình H qua đường thẳng d cũng thuộc hình H( ta nói hình có trục đối xúng)
1/ĐỐI XỨNG TÂM
2/ Hai hình đối xứng qua tâm o.
3/ Hình có tâm đối xứng:
Hai điểm gọi là đối xứng qua điểm o nếu o là trung điểm d0oạn thẳng nối hai điểm đó .
*Hai hình gọi là đối xứng qua điểm o nếu mỗi điểm thuộc hình nàyđối xứng với 1 điểm thuộc hình kiaqua điểm o và ngược lại.
* Diểm O gọi là tâm đối xứng của hình H nếu điểm đối xứng với mỗi điểm thuộc hình H qua điểm Ocũng thuộc hình H
1/ Nếu: 
Thì M,M’ đối xứng qua o
2/ ĐL:
Hình thang có 1 trục đối xứng là đường thẳng qua trung điểm hai cạnh đáy
3/ ĐL:
Giao điểm hai đường chéo là tâm đối xứng của hình bình hành đó
HÌNH
ĐỊNH NGHĨA
TÍNH CHẤT
ĐỊNH LÝ
DẤU HIỆU
HÌNH BÌNH HÀNH:
Hình bình hành là tứ giác có các cạnh đối song song
Hình bình hành ĩ
Hình bình hành ABCD
=> AB//CD ; AD//BC
 Và AB=CD;AD=BC
=>
=>
* O là tâm đối xứng
a) các cạnh đối //
b) các góc đối bằng nhau
c) hai đường chéo cắt nhau tại trung điểm mổi đường
Tứ giác có 1 trong 5 điều sau là h-b-h
1) cacù cạnh đối //
2) cá cạnh đối = nhau
3) hai cạnh đối // và bằng nhau
4) các góc đối bằng nhau
5) hai đường chéo cắt nhau tại trung điểm mỗi đường.
Hình chữ nhật:
Hình chữ nhật là tứ giác có 4 góc vuông
ABCD là h-ch-nh ĩ
.
* Hình chữ nhật có tất cả các tính chất hình b-h và thang cân
* Hai đường chéo bằng nhau và cắt nhau tại trung điểm mỗi đường
1) Trong tam giác vuông ,đường trung tuyến ứng cạnh huyền bằng nửa cạnh ấy
2) Trong một tam giác nếu có trung tuyến ứng với một cạnh mà bằng nửa cạnh ấy thì tam giác đó vuông.
1) tứ giác có 3 góc vuông là h ch nh
2) thang cân có 1 góc vuông là h-ch-nh
3) bình hành có 1 góc vuông là h-ch-nh
4) bình hành có 2 đường chéo bằng nhau là h-ch-nhật
S = 
 S = a.b
S = 
S = a.h
S = 
 S = (AC.DB)1/2
 = AH.DC
S =(AC.DB):2
 B
 a d
 D
S = a2= DB2/2
(hình vuông)