Giáo án tự chọn Toán học Lớp 6 - Năm học 2011-2012 - Phạm Văn Nam

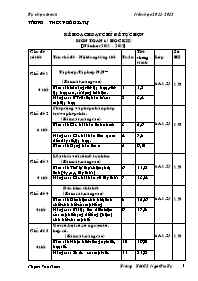
Tr­êng THCS Ng« gia Tù
KÕ ho¹ch d¹y chñ ®Ò tù chän
M«n to¸n 6 ( häc k× I)
 (N¨m häc 2011 - 2012)
Chñ ®Ò 
sè tiÕt
Tªn chñ ®Ò - Néi dung tõng tiÕt
TuÇn
TiÕt ch­¬ng tr×nh
Líp
Sè HS
Chñ ®Ò 1
 4 tiÕt
 TËp hîp, TËp hîp N, N 
 (B¸m s¸t, n©ng cao)
6A1,2,3
138
B¸m s¸t: kÜ n¨ng viÕt tËp hîp, viÕt tËp hîp con, sö dông kÝ hiÖu.
1
1,2
N©ng cao: BTvÒ sè phÇn tö cña mét tËp hîp
2
3,4
Chñ ®Ò 2
 6 tiÕt
PhÐp céng vµ phÐp nh©n- phÐp trõ vµ phÐp chia. 
 (B¸m s¸t, n©ng cao)
6A1,2,3
138
B¸m s¸t: C¸c bµi to¸n tÝnh nhanh
3
5,6
N©ng cao: C¸c bµi to¸n liªn quan dÕn d·y sè, tËp hîp.
4
7,8
B¸m s¸t: D¹ng to¸n t×m x
5
9,10
Chñ ®Ò 3
 4 tiÕt
Lòy thõa víi sè mò tù nhiªn
 (B¸m s¸t, n©ng cao)
6A1,2,3
138
B¸m s¸t: Thø tù thùc hiÖn phÐp tÝnh( +,-,x, :, lòy thõa)
6
11,12
N©ng cao: C¸c bµi to¸n vÒ lòy thõa
7
13,14
Chñ ®Ò 4
 4 tiÕt
 DÊu hiÖu chia hÕt
 (B¸m s¸t, n©ng cao)
6A1,2,3
138
B¸m s¸t: DÊu hiÖu chia hÕt, tÝnh chÊt chia hÕt cña mét tæng
8
15,16
N©ng cao: Bµi tËp t×m ®iÒu kiÖn cña mét sè h¹ng ®Ó tæng ( hiÖu) chia hÕt cho mét sè
9
17,18
Chñ ®Ò 5
 4 tiÕt
¦íc sè, béi sè, sè nguyªn tè, 
hîp sè. 
 (B¸m s¸t, n©ng cao)
6A1,2,3
138
B¸m s¸t: NhËn biÕt sè nguyªn tè, hîp sè.
10
19,20
N©ng cao: S« ­íc cña mét sè.
11
21,22
Chñ ®Ò 6
 4 tiÕt
 Ph©n tÝch mét sè ra thõa sè nguyªn tè
 (B¸m s¸t, n©ng cao)
6A1,2,3
138
B¸m s¸t: C¸ch ph©n tÝch mét sè ra thõa sè nguyªn tè.
12
23,24
N©ng cao: BT vÒ c¸ch t×m ­íc cña mét sè.
13
25,26
Chñ ®Ò 7
 4tiÕt
 ¦íc chung, ¦íc chung lín nhÊt 
 (B¸m s¸t, n©ng cao)
6A1,2,3
138
B¸m s¸t: §Þnh nghÜa, tÝnh chÊt
14
27,28
N©ng cao: Bµi tËp vËn dông
15
29,30
Chñ ®Ò 8
 4 tiÕt
Béi chung, béi chung nhá nhÊt.
 (B¸m s¸t, n©ng cao)
6A1,2,3
138
B¸m s¸t: §Þnh nghÜa, tÝnh chÊt 
16
31,32
N©ng cao: Bµi tËp vËn dông 
17
33,34
Chñ ®Ò 9
 4 tiÕt
 §iÓm- ®­êng th¼ng- ®o¹n th¼ng.
 (B¸m s¸t)
6A1,2,3
138
B¸m s¸t: C¸c kh¸i niÖm, vÞ trÝ t­¬ng ®èi cña ®­êng th¼ng, ®o¹n th¼ng.
18
35
B¸m s¸t: RÌn luyÖn vÏ h×nh 
18
36
Ban gi¸m hiÖu	Nhãm tr­ëng
Tr­êng THCS Ng« gia Tù
KÕ ho¹ch d¹y chñ ®Ò tù chän
M«n to¸n 6 ( häc k× II)
 (N¨m häc 2011- 2012)
Chñ ®Ò 
sè tiÕt
Tªn chñ ®Ò - Néi dung tõng tiÕt
TuÇn
TiÕt ch­¬ng tr×nh
Líp
Sè HS
Chñ ®Ò 1
 16 tiÕt
 C¸c phÐp to¸n trªn tËp hîp sè nguyªn 
(B¸m s¸t)
6A1,2,3
138
PhÐp céng c¸c sè nguyªn
20
1,2
PhÐp trõ c¸c sè nguyªn
21
3,4
Quy t¾c dÊu ngoÆc
22
5,6
Quy t¾c dÊu ngoÆc
23
7,8
Quy t¾c chuyÓn vÕ
24
9,10
PhÐp nh©n, tÝnh chÊt cña phÐp nh©n c¸c sè nguyªn
25
11,12
Béi vµ ­íc cña c¸c sè nguyªn
26
13,14
¤n tËp
27
15,16
Chñ ®Ò 2
 6 tiÕt
Gãc
(B¸m s¸t)
6A1,2,3
138
Gãc sè ®o gãc - Sè ®o gãc- Céng sè ®o gãc
28
17,18
VÏ gãc biÕt sè ®o gãc trªn nöa mÆt ph¼ng
29
19,20
Tia ph©n gi¸c cña mét gãc
30
21,22
Chñ ®Ò 3
 14 tiÕt
Ph©n sè
(B¸m s¸t)
6A1,2,3
138
TÝnh chÊt c¬ b¶n cña ph©n sè
31
23,24
PhÐp céng c¸c ph©n sè
32
25,26
PhÐp trõ c¸c ph©n sè
33
27,28
PhÐp nh©n vµ chia c¸c ph©n sè
34
29,30
Phèi hîp c¸c phÐp tÝnh vÒ ph©n sè
35
31,32
Phèi hîp c¸c phÐp tÝnh vÒ ph©n sè 
36
33,34
¤n tËp 
37
35,36
Ban gi¸m hiÖu	Nhãm tr­ëng
Chñ ®Ò 1: TËp hîp – TËp hîp N, tËp hîp N*
Ngày soạn:10/08/2011
Ngày dạy: /08/2011
Tiết 1: Viết tập hợp, viết tập hợp con 
A. Mục tiêu
+ Kiến thức: Ôn tập và khắc sâu các kiến thức về tập hợp.
+ Kĩ năng: Rèn luyện cách viết tập hợp và cách sử dụng các kí hiệu , , .
+ Thái độ: Có thái độ học tập nghiêm túc
B. Phương pháp
Luyện tập rèn luyện kĩ năng.
C. Chuẩn bị: Thước thẳng, bảng phụ.
D. Tiến trình dạy học
I. Ổn định lớp
II. Bài cũ: 
III. Bài mới :
HOẠT ĐỘNG CỦA GV - HS
NỘI DUNG 
 Hoạt động 1
 GV đưa ra hệ thống các câu hỏi, HS trả lời và ôn tập lại các kiến thức đã học nhờ vào các câu hỏi mà GV đưa ra:
?1: Hãy mô tả cách viết một tập hợp? Cho ví dụ.
?2: Để viết một tập hợp, thường có mấy cách? Cho ví dụ.
?3: Hãy viết các tập hợp N, N*. Đó là những tập hợp số gì?
?4: Một tập hợp có thể có bao nhiêu phần tử ? Lấy ví dụ minh hoạ.
?5: Khi nào thì tập hợp A được gọi là tập hợp con của tập hợp B ? Viết kí hiệu thể hiện tập hợp A là một tập hợp con của tập hợp B. Cho ví dụ.
?6: Khi nào thi ta nói hai tập hợp A và B là bằng nhau? Cho ví dụ.
I. Lý thuyết.
1. Tập hợp.
+ Cách viết một tập hợp:
+ Hai cách viết tập hợp:
 VD: Khi viết tập hợp A các số tự nhiên nhỏ hơn 5, ta viết:
 C1 : A = {0, 1, 2, 3, 4}.
 (hoặc: A = {1, 0, 4, 3, 2} , ...).
 C2 : A = {x N / x < 5}.
+ Tập N các số tự nhiên:
 N = {0, 1, 2, 3, 4, . . . }.
+ Tập N* các số tự nhiên khác 0:
 N* = {1, 2, 3, 4, . . . }.
+ Số phần tử của một tập hợp:
(có 1, nhiều, vô số, cũng có thể khong có phần tử nào)
 VD: (lấy theo HS)
2. Tập hợp con.
+ Tập hợp con:
+ Kí hiệu tập hợp con:
 Nếu A là tập con của B ta viết:
 A B hoặc B A.
+ VD: (lấy theo HS)
+ Hai tập hợp bằng nhau:
 Nếu A B và B A thì A và B là hai tập hợp bằng nhau, kí hiệu: A = B.
VD: (lấy theo HS)
 Hoạt động 2: 
 GV đưa ra hệ thống các bài tập, tổ chức hướng dẫn cho HS thực hiện các hoạt động học tập:
Bài 1: Viết tập hợp A các số tự nhiên lớn hơn 7 và nhỏ hơn 12 bằng hai cách, sau đó điền các kí hiệu thích hợp vào ô trống:
 9 A ; 14 A.
Bài 2: Viết tập hợp B các chữ cái có trong từ: “SÔNG HỒNG” 
Bài 3: Cho hai tập hợp:
 A = {m, n, p} ; B = {m, x, y}
Điền kí hiệu thích hợp vào ô vuông:
n A ; p B ; m B	
- GV hướng dẫn HS thực hiện, sau đó yêu cầu 3 HS lên bảng trình bày lời giải
- HS cả lớp thực hiện, sau đó nhận xét bài làm của bạn
- GV nhận xét chuẩn hoá kết quả
Bài 4: Viết các tập hợp sau và cho biết mỗi tập hợp có bao nhiêu phần tử:
a) Tập hợp A các số tự nhiên x mà:
 x – 5 = 13
b) Tập hợp B các số tự nhiên x mà: 
 x + 8 = 8
c) Tập hợp C các số tự nhiên x mà:
 x . 0 = 0
d) Tập hợp D các số tự nhiên x mà:
 x . 0 = 7
- GV hướng dẫn HS thực hiện, sau đó 4 HS lên bảng viết kết quả
- HS nhận xét, Gv chuẩn hoá kết quả.
Bài 5: Viết các tập hợp sau và cho biết mỗi tập hợp có bao nhiêu phần tử:
a) Tập hợp các số tự nhiên không vượt quá 50.
b) Tập hợp các số tự nhiên lớn hơn 8 nhưng nhỏ hơn 9.
- GV hướng dẫn:
- 2 HS lên bảng viết
- HS nhận xét bổ xung, GV nhận xét chuẩn hoá kết quả.
Bài 6: Tính số phần tử của các tập hợp sau:
A = {40; 41; 42; . . . ; 100}
B = {10; 12; 14; . . . ; 98}
C= {35; 37; 39; . . . ; 105}
- GV hướng dẫn: (áp dụng các công thức đã học ở bài tập số 21, 22- sgk tr.14)
- HS thực hiện, sau đó 3 HS lên bảng trình bày lời giải
- HS nhận xét sau đó GV nhận xét chuẩn hoá kết quả.
Bài 7: cho hai tập hợp: 
A = {a, b, c, d} , B = {a, b}.
a) Dùng kí hiệu để thể hiện quan hệ của hai tập hợp A và B.
b) Dùng hình vẽ minh họa hai tập hợp A và B.
c) Viết ra các tập hợp con của tập hợp A sao cho mỗi tập hợp con đó có hai phần tử.
Bài 8: Cho ví dụ hai tập hợp M và N mà :
 M N và N M.
- GV h­íng dÉn lÊy vÝ dô
- HS lÊy vÝ dô sau ®ã nªu lªn, c¸c HS kh¸c nhËn xÐt bæ xung, GV chuÈn ho¸ kÕt qu¶.
II. Bµi tËp.
Bµi 1:
C1 : A = {8, 9, 10, 11}
C2 : A = {x N / 7 < x < 12}
 9 A ; 14 A.
Bµi 2: 
 B = {S, ¤, N, H, G}
Bµi 3:
 n A ; p B ; m A, B
Bµi 4:
A = {18} : cã 1 phÇn tö;
B = {0} : cã 1 phÇn tö:
C = {0, 1, 2, 3, 4, . . . } :cã v« sè phÇn tö;
 Kh«ng cã sè tù nhiªn x nµo mµ 
 x . 0 = 7 , vËy D = 
Bµi 5: 
a) N = {0; 1; 2; 3; . . .; 50} : cã 50 phÇn tö
b) Kh«ng cã sè tù nhiªn nµo võa lín h¬n 8 võa nhá h¬n 9, vËy lµ tËp : .
Bµi 6: 
a) Sè phÇn tö cña tËp hîp A lµ:
 100 – 40 + 1 = 61(phÇn tö)
b) Sè phÇn tö cña tËp hîp B lµ:
 (98 - 10) : 2 + 1 = 45(phÇn tö)
c) Sè phÇn tö cña tËp hîp B lµ:
 (105 - 35) : 2 + 1 = 36(phÇn tö)
Bµi 7:
a) B A
c) {a, b}; {a, c}; {a, d}; {b, c}; {b, d};
{c, d}.
Bµi 8:
(lµm theo bµi cña HS)
Ho¹t ®éng 3: H­íng dÉn vÒ nhµ
HS «n tËp vµ xem l¹i c¸c bµi tËp ®· ®­îc lµm.
Lµm c¸c bµi tËp sau:
Bµi 9: Cho c¸c tËp hîp sau:
A = {x N / 20 < x < 21}
 B = {x N* / x < 4 }
C = {x N / 35 x 38}
D = { x N / x 0}
a) Viết các tập hơp sau bằng cách liệt kê các phần tử
b) Mỗi tập hợp trên có bao nhiêu phần tử
 c) Dùng kí hiệu để thể hiện mối quan hệ của các tập hợp trên
Ngày soạn:19/08/2011
Ngày dạy: /08/2011
Tiết 3,4: C¸c bµi tËp vÒ x¸c ®Þnh sè phÇn tö cña mét tËp hîp
Bµi 1: Gäi A lµ tËp hîp c¸c sè tù nhiªn cã 3 ch÷ sè. Hái tËp hîp A cã bao nhiªu phÇn tö?
 H­íng dÉn:
 TËp hîp A cã (999 – 100) + 1 = 900 phÇn tö.
 Bµi 2: H·y tÝnh sè phÇn tö cña c¸c tËp hîp sau:
 a) TËp hîp A c¸c sè tù nhiªn lÎ cã 3 ch÷ sè.
 b) TËp hîp B c¸c sè 2, 5, 8, 11, , 296.
 c) TËp hîp C c¸c sè 7, 11, 15, 19, , 283.
H­íng dÉn:
 a) TËp hîp A cã (999 – 101):2 +1 = 450 phÇn tö.
 b) TËp hîp B cã (296 – 2 ): 3 + 1 = 99 phÇn tö.
 c) TËp hîp C cã (283 – 7 ):4 + 1 = 70 phÇn tö.
Cho HS ph¸t biÓu tæng qu¸t:
 -TËp hîp c¸c sè ch½n tõ sè ch½n a ®Õn sè ch½n b cã (b – a) : 2 + 1 phÇn tö.
 -TËp hîp c¸c sè lÎ tõ sè lÎ m ®Õn sè lÎ n cã (n – m) : 2 + 1 phÇn tö.
 -TËp hîp c¸c sè tõ sè c ®Õn sè d lµ d·y sè c¸c ®Òu, kho¶ng c¸ch gi÷a hai sè liªn 
 tiÕp cña d·y lµ 3 cã (d – c ): 3 + 1 phÇn tö.
Bµi 3: Cha mua cho em mét quyÓn sè tay dµy 256 trang. §Ó tiÖn theo dâi em ®¸nh sè 
 trang tõ 1 ®Õn 256. Hái em ®· ph¶i viÕt bao nhiªu ch÷ sè ®Ó ®¸nh hÕt cuèn sæ tay?
H­íng dÉn:
 - Tõ trang 1 ®Õn trang 9, viÕt 9 sè.
 - Tõ trang 10 ®Õn trang 99 cã 90 trang, viÕt 90 . 2 = 180 ch÷ sè.
 - Tõ trang 100 ®Õn trang 256 cã (256 – 100) + 1 = 157 trang, cÇn viÕt 157 . 3 = 
 471 sè.
 VËy em cÇn viÕt 9 + 180 + 471 = 660 sè.
Bµi 4: C¸c sè tù nhiªn tõ 1000 ®Õn 10000 cã bao nhiªu sè cã ®óng 3 ch÷ sè gièng 
 nhau.
H­íng dÉn:
 - Sè 10000 lµ sè duy nhÊt cã 5 ch÷ sè, sè nµy cã h¬n 3 ch÷ sè gièng nhau nªn kh«ng tho¶ m·n yªu cÇu cña bµi to¸n.
VËy sè cÇn t×m chØ cã thÓ cã d¹ng: , , , víi a b lµ c¸ ch÷ sè.
- XÐt sè d¹ng , ch÷ sè a cã 9 c¸ch chän ( a 0) cã 8 c¸ch chän ®Ó b kh¸c a.
VËy cã 9 . 8 = 72 sè cã d¹ng .
LËp luËn t­¬ng tù ta thÊy c¸c d¹ng cßn l¹i ®Òu cã 72 sè. Suy ta tÊt c¶ c¸c sè tõ 1000 ®Õn 10000 cã ®óng 3 ch÷ sè gièng nhau gåm 72.4 =288 Sè 
Chñ ®Ò 2: PHÐP CéNG Vµ PHÐP NH¢N - PHÐP TRõ Vµ PHÐP CHIA
Ngày soạn:28/08/2011
Ngày dạy: /09/2011
Tiết 5,6: Các bài toán tính nhanh
A. Mục tiêu
+ Kiến thức:Ôn tập, bổ xung và hệ thống lại các kiến thức đã được học về phép cộng và phép nhân.
+ Kĩ năng: Rèn luyện các kĩ năng tính toán, kĩ năng thực hiện các phép tính nhanh nhờ áp dụng các tính chất của phép toán.
- Rèn luyện tư duy nhạy bén linh hoạt trong cách biến đổi các phép toán.
+ Thái độ: Nâng cao ý thức tự học, tự rèn luyện.
B. Phương pháp 
Luyện tập rèn luyện kĩ năng thông qua hệ thống các câu hỏi và bài tập.
C. Chuẩn bị: thước thẳng, bảng phụ
D ... 9: T×m A biÕt:
H­íng dÉn 
Ta cã (A - ).10 = A. VËy 10A – 7 = A suy ra 9A = 7 hay A = 
Bµi 10: Lóc 6 giê 50 phót b¹n ViÖt ®i xe ®¹p tõ A ®Õn B víi vËn tèc 15 km/h. Lóc 7 giê 10 phót b¹n Nam ®i xe ®¹p tõ B ®Õn A víi vËn tèc 12 km/h/ Hai b¹n gÆp nhau ë C lóc 7 giê 30 phót. TÝnh qu·ng ®­êng AB.
H­íng dÉn
Thêi gian ViÖt ®i lµ: 
7 giê 30 phót – 6 giê 50 phót = 40 phót = giê
Qu·ng ®­êng ViÖt ®i lµ:
=10 (km)
Thêi gian Nam ®· ®i lµ:
7 giê 30 phót – 7 giê 10 phót = 20 phót = giê
Qu·ng ®­êng Nam ®· ®i lµ (km)
Bµi 11: . TÝnh gi¸ trÞ cña biÓu thøc:
 biÕt x + y = -z
H­íng dÉn
Bµi 12: TÝnh gÝ trÞ c¸c biÓu thøc A, B, C råi t×m sè nghÞch ®¶o cña chóng.
a/ A = 
b/ B = 
c/ C = 
H­íng dÉn
a/ A = nªn sè nghÞch ®¶o cña A lµ 2003
b/ B = nªn sè nghÞc ®¶o c¶u B lµ 
c/ C = nªn sè nghÞch ®¶o cña C lµ 
Bµi 13: Thùc hiÖn phÐp tÝnh chia sau:
a/ ;
b/ 
c/ 
d/ 
Bµi 14: T×m x biÕt:
a/ 
b/ 
c/ 
H­íng dÉn
a/ 
b/ 
c/ 
Bµi 15: §ång hå chØ 6 giê. Hái sau bao l©u kim phót vµ kim giê l¹i gÆp nhau?
H­íng dÉn
Lóc 6 giê hai kim giê vµ phót c¸ch nhau 1/ 2 vßng trßn.
VËn tèc cña kim phót lµ: (vßng/h)
HiÖu vËn tèc gi÷a kim phót vµ kim giê lµ: 1- = (vßng/h)
VËy thêi gian hai kim gÆp nhau lµ: = (giê)
Bµi 16: Mét can« xu«i dßng tõ A ®Õn B mÊt 2 giê vµ ng­îc dßng tõ B vÒ A mÊt 2 giê 30 phót. Hái mét ®¸m bÌo tr«i tõ A ®Õn B mÊt bao l©u?
H­íng dÉn
VËn tèc xu«i dßng cña can« lµ: (km/h)
V©n tèc ng­îc dßng cña can« lµ: (km/h)
VËn tèc dßng n­íc lµ: : 2 = : 2 = (km/h)
VËn tèc bÌo tr«i b»ng vËn tèc dßng n­íc, nªn thêi gian bÌo tr«i tõ A ®Õn B lµ: 
AB: = AB : = 20 (giê)
================
Chuyªnn ®Ò : SO S¸NH PH¢N Sè
:
	§Ó so s¸nh 2 ph©n sè , tïy theo mét sè tr­êng hîp cô thÓ cña ®Æc ®iÓm c¸c ph©n sè , ta cã thÓ sö dông nhiÒu c¸ch tÝnh nhanh vµ hîp lÝ .TÝnh chÊt b¾c cÇu cña thø tù th­êng ®­îc sö dông (), trong ®ã ph¸t hiÖn ra mét sè trung gian ®Ó lµm cÇu nèi lµ rÊt quan träng.Sau ®©y t«i xin giíi thiÖu mét sè ph­¬ng ph¸p so s¸nh ph©n sè 
PHÇN I: C¸C PH¦¥NG PH¸P SO S¸NH .
Quy ®ång mÉu d­¬ng råi so s¸nh c¸c tö :tö nµo lín h¬n th× ph©n sè ®ã lín h¬n 
I/C¸CH 1: 
VÝ dô : So s¸nh ?
	Ta viÕt : ; 
Quy ®ång tö d­¬ng råi so s¸nh c¸c mÉu cã cïng dÊu “+” hay cïng dÊu “-“: mÉu nµo nhá h¬n th× ph©n sè ®ã lín h¬n .
Chó ý :Ph¶i viÕt ph©n sè d­íi mÉu d­¬ng .
II/C¸CH 2: 
VÝ dô 1 : 
VÝ dô 2: So s¸nh ?
Ta cã : ; 	
	VÝ dô 3: So s¸nh ? 
Ta cã : ; 	
	Chó ý : Khi quy ®ång tö c¸c ph©n sè th× ph¶i viÕt c¸c tö d­¬ng .
(TÝch chÐo víi c¸c mÉu b vµ d ®Òu lµ d­¬ng )
 +NÕu a.d>b.c th× + NÕu a.d<b.c th× ; + NÕu a.d=b.c th× 
III/C¸CH 3: 
	VÝ dô 1: 
	VÝ dô 2:
 VÝ dô 3:So s¸nh Ta viÕt ; V× tÝch chÐo –3.5 > -4.4 nªn 
	Chó ý : Ph¶i viÕt c¸c mÉu cña c¸c ph©n sè lµ c¸c mÉu d­¬ng 
v× ch¼ng h¹n do 3.5 < -4.(-4) lµ sai 
Dïng sè hoÆc ph©n sè lµm trung gian .
IV/C¸CH 4: 
Dïng sè 1 lµm trung gian:
NÕu 
NÕu mµ M > N th× 
M,N lµ phÇn thõa so víi 1 cña 2 ph©n sè ®· cho .
Ph©n sè nµo cã phÇn thõa lín h¬n th× ph©n sè ®ã lín h¬n.
NÕu mµ M > N th× 
M,N lµ phÇn thiÕu hay phÇn bï ®Õn ®¬n vÞ cña 2 ph©n sè ®ã.
Ph©n sè nµo cã phÇn bï lín h¬n th× ph©n sè ®ã nhá h¬n.
Bµi tËp ¸p dông :
Bµi tËp 1: So s¸nh 
Ta cã : ; 
Bµi tËp 2: So s¸nh 
Ta cã : ; 	
 Bµi tËp 3 : So s¸nh Ta cã 
Dïng 1 ph©n sè lµm trung gian:(Ph©n sè nµy cã tö lµ tö cña ph©n sè thø nhÊt , cã mÉu lµ mÉu cña ph©n sè thø hai)
VÝ dô : §Ó so s¸nh ta xÐt ph©n sè trung gian .
	V× 
*NhËn xÐt : Trong hai ph©n sè , ph©n sè nµo võa cã tö lín h¬n , võa cã mÉu nhá h¬n th× ph©n sè ®ã lín h¬n (®iÒu kiÖn c¸c tö vµ mÉu ®Òu d­¬ng ).
*TÝnh b¾c cÇu : 
Bµi tËp ¸p dông :
Bµi tËp 1: So s¸nh 
-XÐt ph©n sè trung gian lµ , ta thÊy 
-HoÆc xÐt sè trung gian lµ , ta thÊy 
Bµi tËp 2: So s¸nh 
Dïng ph©n sè trung gian lµ
Ta cã : 
Bµi tËp 3: (Tù gi¶i) So s¸nh c¸c ph©n sè sau:
 e) 
 f) 
 g) 
 h) 
(H­íng dÉn : Tõ c©u ac :XÐt ph©n sè trung gian.
 	Tõ c©u dh :XÐt phÇn bï ®Õn ®¬n vÞ )
Dïng ph©n sè xÊp xØ lµm ph©n sè trung gian.
VÝ dô : So s¸nh 
Ta thÊy c¶ hai ph©n sè ®· cho ®Òu xÊp xØ víi ph©n sè trung gian lµ.
Ta cã : 
Bµi tËp ¸p dông :
Dïng ph©n sè xÊp xØ lµm ph©n sè trung gian ®Ó so s¸nh :
Dïng tÝnh chÊt sau víi m0 : 
V/ C¸CH 5:
Bµi tËp 1: So s¸nh 
Ta cã : (v× tö < mÉu) 	
VËy A < B .
Bµi tËp 2: So s¸nh 
Ta cã : Céng theo vÕ ta cã kÕt qu¶ M > N.
Bµi tËp 3:So s¸nh ?
Gi¶i: (¸p dông )
§æi ph©n sè lín h¬n ®¬n vÞ ra hçn sè ®Ó so s¸nh :
+Hçn sè nµo cã phÇn nguyªn lín h¬n th× hçn sè ®ã lín h¬n.
+NÕu phÇn nguyªn b»ng nhau th× xÐt so s¸nh c¸c ph©n sè kÌm theo.
VI/C¸CH 6: 
Bµi tËp 1:S¾p xÕp c¸c ph©n sè theo thø tù t¨ng dÇn.
Gi¶i: ®æi ra hçn sè : 
Ta thÊy: nªn .
Bµi tËp 2: So s¸nh 
Gi¶i: mµ 
Bµi tËp 3: S¾p xÕp c¸c ph©n sè theo thø tù t¨ng dÇn.
Gi¶i: XÐt c¸c ph©n sè nghÞch ®¶o: , ®æi ra hçn sè lµ : 
Ta thÊy: 
Bµi tËp 4: So s¸nh c¸c ph©n sè : ?
H­íng dÉn gi¶i: Rót gän A=1 , ®æi B;C ra hçn sè A<B<C.
Bµi tËp 5: So s¸nh 
H­íng dÉn gi¶i:-Rót gän 
( Chó ý: 690=138.5&548=137.4 )
Bµi tËp 6: (Tù gi¶i) S¾p xÕp c¸c ph©n sè theo thø tù gi¶m dÇn.
PHÇN II: C¸C BµI TËP TæNG HîP .
	Bµi tËp 1: So s¸nh c¸c ph©n sè sau b»ng c¸ch hîp lý:
	(Gîi ý: a) Quy ®ång tö c) XÐt phÇn bï , chó ý :
	d)Chó ý: XÐt phÇn bï ®Õn ®¬n vÞ 
	e)Chó ý: phÇn bï ®Õn ®¬n vÞ lµ:)
Bµi tËp 2: Kh«ng thùc hiÖn phÐp tÝnh ë mÉu , h·y dïng tÝnh chÊt cña ph©n sè ®Ó so s¸nh c¸c ph©n sè sau: 
H­íng dÉn gi¶i:Sö dông tÝnh chÊt a(b + c)= ab + ac
+ViÕt 244.395=(243+1).395=243.395+395
+ViÕt 423134.846267=(423133+1).846267=.. .
+KÕt qu¶ A=B=1
(Gîi ý: lµm nh­ c©u a ë trªn ,kÕt qu¶ M=N=1,P>1)
Bµi tËp 3: So s¸nh 
Gîi ý: 7000=7.103 ,rót gän 
Bµi tËp 4: So s¸nh 
Gîi ý: ChØ tÝnh 
Tõ ®ã kÕt luËn dÔ dµng : A < B
Bµi tËp 5:So s¸nh ?
Gîi ý: 1919=19.101 & 191919=19.10101 ; KÕt qu¶ M>N
	Më réng : 123123123=123.1001001 ;...
 Bµi tËp 6: So s¸nh 
	Gîi ý: +C¸ch 1: Sö dông ; chó ý : 
	 +C¸ch 2: Rót gän ph©n sè sau cho 101.
	 Bµi tËp 7: Cho a,m,n N* .H·y so s¸nh : 
	 Gi¶i: 	
	 Muèn so s¸nh A & B ,ta so s¸nh & b»ng c¸ch xÐt c¸c tr­êng hîp sau:
Víi a=1 th× am = an A=B
Víi a0:
NÕu m= n th× am = an A=B
NÕu m< n th× am < an A < B
NÕu m > n th× am > an A >B
	Bµi tËp 8: So s¸nh P vµ Q, biÕt r»ng: ?
	VËy P = Q
	Bµi tËp 9: So s¸nh 
	Gi¶i: Rót gän 
	VËy M = N
	Bµi tËp 10: S¾p xÕp c¸c ph©n sè theo thø tù t¨ng dÇn ?
	 Gîi ý: Quy ®ång tö råi so s¸nh .
	 Bµi tËp 11: T×m c¸c sè nguyªn x,y biÕt: ?
	 Gîi ý : Quy ®ång mÉu , ta ®­îc 2 < 3x < 4y < 9
	 Do ®ã x=y=1 hay x=1 ; y=2 hay x=y=2.
	 Bµi tËp 12: So s¸nh 
	 Gi¶i: Ap dông c«ng thøc: 
	 Chän lµm ph©n sè trung gian ,so s¸nh > C > D.
	 Bµi tËp 13: Cho 
	a)Chøng minh: M < N b) T×m tÝch M.N c) Chøng minh: 
	 Gi¶i: NhËn xÐt M vµ N ®Òu cã 45 thõa sè
	a)Vµ	 nªn M < N
	b) TÝch M.N
	c)V× M.N mµ M < N nªn ta suy ra ®­îc : M.M <<
	tøc lµ M.M < . M < 
	 Bµi tËp 14: Cho tæng : .Chøng minh: 
Gi¶i: Tæng S cã 30 sè h¹ng , cø nhãm 10 sè h¹ng lµm thµnh mét nhãm .Gi÷ nguyªn tö , nÕu thay mÉu b»ng mét mÉu kh¸c lín h¬n th× gi¸ trÞ cña ph©n sè sÏ gi¶m ®i. Ng­îc l¹i , nÕu thay mÉu b»ng mét mÉu kh¸c nhá h¬n th× gi¸ trÞ cña ph©n sè sÏ t¨ng lªn.
	 Ta cã : 
	hay tõc lµ: VËy (1)
	 MÆt kh¸c: 
	 tøc lµ : VËy (2).
	 Tõ (1) vµ (2) suy ra :®pcm.
ĐỀ SỐ HỌC 6 NÂNG CAO sè1
1. Viết các tập hợp sau bằng cách liệt kê các phần tử của nó:
	a) Tập hợp A các số tự nhiên có hai chữ số trong đó chữ số hàng chục lớn hơn chữ số hàng đơn vị là 3.
	b) Tập hợp B các số tự nhiên có ba chữ số mà tổng các chữ số bằng 5.
2. * Ghi số nhỏ nhất có:	a) chín chữ số
	b) n chữ số (nÎ N*)
	c) mười chữ số khác nhau
 ** Ghi số lớn nhất có:	a) chín chữ số
	b) n chữ số (nÎ N*)
	c) mười chữ số khác nhau
3. Người ta viết liên tiếp các số tự nhiên thành dãy số sau:
 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 ...Hỏi:
	a) Chữ số hàng đơn vị của số 52 đứng ở hàng thứ mấy?
	b) Chữ số đứng ở hàng thứ 873 là chữ số gì? Chữ số đó của số tự nhiên nào?
4. Điền kí hiệu thích hợp vào ô vuông:
	a) 2 c {1; 2; 6}	e) Æ c {a}
	b) 3 c {1; 2; 6}	f) 0 c {0}
	c) {1} c {1; 2; 6}	g) {3; 4} c N
	d) {2;1; 6} c {1; 2; 6}	h) 0 c N*
5. Trong đợt thi đua "Bông hoa điểm 10" mừng ngày Nhà giáo Việt Nam - Lớp 6/1 có 45 bạn đạt từ 1 điểm 10 trở lên, 38 bạn đạt từ 2 điểm 10 trở lên, 15 bạn đạt từ 3 
điểm 10 trở lên, 9 bạn đạt 4 điểm 10, không có ai đạt trên 4 điểm 10. Hỏi trong đợt thi đua đó, lớp 6/1 có tất cả bao nhiêu điểm 10?
6. Trong đợt dự thi "Hội khoẻ Phù Đổng", kết quả điều tra ở một lớp cho thấy; có 25 học sinh thích bóng đá, 22 học sinh thích điền kinh, 24 học sinh thích cầu lông, 14 học sinh thích bóng đá và điền kinh, 16 học sinh thích bóng đá và cầu lông, 15 học sinh thích cầu lông và điền kinh, 9 học sinh thích cả 3 môn, còn lại là 6 học sinh thích cờ vua. Hỏi lớp đó có bao nhiêu học sinh?
7. Muốn viết tất cả các số tự nhiên từ 1 đến 1000 phải dùng bao nhiêu chữ số 5?
8. Điền các chữ số thích hợp vào ô trống để tổng ba chữ số liền nhau bằng 23:
6
8
9. Tìm số có hai chữ số sao cho số đó lớn hơn 6 lần tổng các chữ số của nó là 2 đơn vị.
10. Tìm số bị chia và số chia nhỏ nhất để thương của phép chia là 15 và số dư là 36.
11. Em hãy đặt các dấu (+) và dấu (-) vào giữa các chữ số của số 1 2 3 4 5 6 7 8 9 (có thể ghép chúng lại với nhau) để kết quả của phép tính bằng 200.
12. Tìm số tự nhiên có hai chữ số, biết rằng tổng các chữ số của nó là 11 và nếu đổi chỗ hai chữ số đó cho nhau ta được số mới hơn số cũ 63 đơn vị.
13. Một phép chia có tổng của số bị chia và số chia là 97. Biết rằng thương là 4 và số dư là 7. Tìm số bị chia và số chia.
14. So sánh: 21000 và 5400
15. Tìm n Î N, biết:
	a) 2n . 8 = 512	b) (2n + 1)3 = 729
16. Tính giá trị của biểu thức:
	a) 39 : 37 + 5 . 22	b) 23 . 32 - 516 : 514
c)
47. 34 . 96
 613
d)
216 + 28
213 + 25
17. Tìm x, y Î N, biết rằng: 2x + 242 = 3y 
18. Tìm x Î N, biết:
	a) 1440 : [41 - (2x - 5)] = 24 . 3
	b) 5.[225 - (x - 10)] -125 = 0
19. Tính giá trị của các biểu thức sau:
	a) [545 - (45 + 4.25)] : 50 - 2000 : 250 + 215 : 213
	b) [504 - (25.8 + 70)] : 9 - 15 + 190
	c) 5 . {26 - [3.(5 + 2.5) + 15] : 15}
	d) [1104 - (25.8 + 40)] : 9 + 316 : 312
20. Tìm x biết:
	a) (x - 15) : 5 + 22 = 24
	b) 42 - (2x + 32) + 12 : 2 = 6
	c) 134 - 2{156 - 6.[54 - 2.(9 + 6)]}. x = 86
21. Xét xem:
	a) 20022003 + 20032004 có chia hết cho 2 không?
	b) 34n - 6 có chia hết cho 5 không? (n Î N*)
	c) 20012002 - 1 có chia hết cho 10 không?
22. Tìm x, y để số chia hết cho cả 2 và 3, và chia cho 5 dư 2.
23. Viết số tự nhiên nhỏ nhất có năm chữ số, tận cùng bằng 6 và chia hết cho 9.