Giáo án Hình học Lớp 8 - Tiết 24: Ôn tập chương I
III. CÁC HOẠT ĐỘNG DẠY VÀ HỌC :
A. HOẠT ĐỘNG 1 : Ổn địng lớp.
B. HOẠT ĐỘNG 2 : Kiểm tra bài cũ :
HS1 : Nêu các tính chất của hình bình hành và các dấu hiệu nhận biết hình bình hành?
HS2 : Nêu các tính chất của hình thoi và các dấu hiệu nhận biết hìng thoi?
HS3 : Nêu các tính chất và dấu hiệu nhận biết của hình vuông ?
C . HOẠT ĐỘNG 3 :Tiền hành ôn tập:
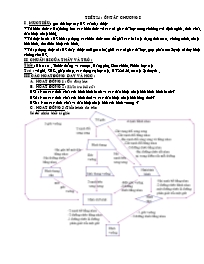
Sơ đồ nhận biết tứ giác
TG Hoạt động của thầy Hoạt động của trò
GV : Hãy trả lời các câu hỏi về lý thuyết trong phần câu hỏi ôn tập?
GV chốt lại các câu hỏi nhanh.
BT 87/111 SGK:
? Hãy nhìn vào sơ đồ hình 109 để điền vào chổ trống?
GV : Chốt lại các câu trả lời.
BT 88/111 SGK.
Hãy vẽ hình và ghi GT/KL của bài?
Nếu ABCD là một tứ giác bất kỳ thì EFGH là hình gì? Vì sao?
Vậy EFGH là hình chữ nhật khi ABCD có thêm điều kiện nào? Vì sao?
EFGH là hình thoi khi nào? Vì sao?
EFGH là hình vuông khi nào? Vì sao?
Hãy trình bày bài làm.
Lưu ý : Trước hết ta phải chứng minh EFGH là hình bình hành rồi mới đi vào các câu a, câu b, câu c.
BT 89/111 SGK.
Hướng dẫn học sinh làm câu a,b
HS trả lời lần lượt các câu hỏi theo SGK.
BT 87/111 SGK:
HS trả lời bằng miệng tại chổ và nhận xét.
BT 88/111 SGK.
GT Tứ giác ABCD
EA = EB;FB=FC
GC=GD;HD=HA
KL ABCD có điều
Kiện gì thì :
a.EFGH là HCN.
b. EFGH là HT.
c. EFGH là HV.
Ta có : EA = EB ; FB=FC; GC=GD ; HD=HA.
Nên : EF // AC; HG // AC; EH // BD; FG // BD.
( Theo T/C đường trung bình).
Suy ra : EF // HG ; EH // GF.
Hay EFGH là hình bình hành.
a. Để EFGH là hình chữ nhật thì phải có một trong bốn góc tại E, F, G, H bằng 900 .
Hay ABCD phải có : AC BD.
b. EFGH là hình thoi khi có : EF=FG=GH=HE
Mà EF = HG = ; EH = FG =
Nên ABCD phải có thêm điều kiện là : AC = BD.
c. EFGH là hình vuông khi EFGH là hình chữ nhật vừa là hình thoi hay : ABCD phải có thêm điều kiện là AC BD và AC = BD.
BT 89/111 SGK.
a/ Chứng minh rằng điểm E đối xứng với điểm M qua AB
Ta có MD là đường trung bình của ABC
MD // AC.Do AC AB nên MDAB
Ta có:AB là đường trung trực của ME nên E đối xứng với M qua AB.
b/ Các tứ giác AEMC ,AEBM là hình gì?
Ta có EM //AC ; EM= AC ( vì cùng bằng 2DM)
Nên: AEMC là hình bình hành.
Tứ giác AEBM là hình thoi vì:AEBM là hình bình hành có hai đường chéo cắt nhau tại trung điểm của mỗi đường.Hình bình hành AEBM có ABEM nên là hình thoi.
TIẾT 24 : ÔN TẬP CHƯƠNG I I . MỤC TIÊU : qua tiết học này HS cần đạt được * Về kiến thức :- Hệ thống hoá các kiến thức về các tứ giác đã học trong chương (về định nghĩa, tính chất, dấu hiệu nhận biết). * Về thực hành : HS biết áp dụng các kiến thức trên để giải các bài tập dạng tính toán, chứng minh, nhận biết hình, tìm điều kiện của hình. * Về áp dụng thực tế : HS thấy được mối quan hệ giữa các tứ giác đã học, góp phần rèn luyện tư duy biện chứng cho HS. II . CHUẨN BỊ CỦA THẦY VÀ TRÒ : Thầy : Giáo án , Thước thẳng và compa, Bảng phụ, Đèn chiếu, Phiếu học tập Trò : vở ghi, SGK, giấp nháp, các dụng cụ học tập, BT 88/152, ôn tập lý thuyết . III. CÁC HOẠT ĐỘNG DẠY VÀ HỌC : HOẠT ĐỘNG 1 : Ổn địng lớp. HOẠT ĐỘNG 2 : Kiểm tra bài cũ : HS1 : Nêu các tính chất của hình bình hành và các dấu hiệu nhận biết hình bình hành? HS2 : Nêu các tính chất của hình thoi và các dấu hiệu nhận biết hìng thoi? HS3 : Nêu các tính chất và dấu hiệu nhận biết của hình vuông ? C . HOẠT ĐỘNG 3 :Tiền hành ôn tập: Sơ đồ nhận biết tứ giác TG Hoạt động của thầy Hoạt động của trò GV : Hãy trả lời các câu hỏi về lý thuyết trong phần câu hỏi ôn tập? GV chốt lại các câu hỏi nhanh. BT 87/111 SGK: ? Hãy nhìn vào sơ đồ hình 109 để điền vào chổ trống? GV : Chốt lại các câu trả lời. BT 88/111 SGK. Hãy vẽ hình và ghi GT/KL của bài? Nếu ABCD là một tứ giác bất kỳ thì EFGH là hình gì? Vì sao? Vậy EFGH là hình chữ nhật khi ABCD có thêm điều kiện nào? Vì sao? EFGH là hình thoi khi nào? Vì sao? EFGH là hình vuông khi nào? Vì sao? Hãy trình bày bài làm. Lưu ý : Trước hết ta phải chứng minh EFGH là hình bình hành rồi mới đi vào các câu a, câu b, câu c. BT 89/111 SGK. Hướng dẫn học sinh làm câu a,b HS trả lời lần lượt các câu hỏi theo SGK. BT 87/111 SGK: HS trả lời bằng miệng tại chổ và nhận xét. BT 88/111 SGK. GT Tứ giác ABCD EA = EB;FB=FC GC=GD;HD=HA KL ABCD có điều Kiện gì thì : a.EFGH là HCN. b. EFGH là HT. c. EFGH là HV. Ta có : EA = EB ; FB=FC; GC=GD ; HD=HA. Nên : EF // AC; HG // AC; EH // BD; FG // BD. ( Theo T/C đường trung bình). Suy ra : EF // HG ; EH // GF. Hay EFGH là hình bình hành. a. Để EFGH là hình chữ nhật thì phải có một trong bốn góc tại E, F, G, H bằng 900 . Hay ABCD phải có : AC ^ BD. b. EFGH là hình thoi khi có : EF=FG=GH=HE Mà EF = HG = ; EH = FG = Nên ABCD phải có thêm điều kiện là : AC = BD. c. EFGH là hình vuông khi EFGH là hình chữ nhật vừa là hình thoi hay : ABCD phải có thêm điều kiện là AC ^ BD và AC = BD. BT 89/111 SGK. a/ Chứng minh rằng điểm E đối xứng với điểm M qua AB Ta có MD là đường trung bình của rABC MD // AC.Do AC ^AB nên MD^AB Ta có:AB là đường trung trực của ME nên E đối xứng với M qua AB. b/ Các tứ giác AEMC ,AEBM là hình gì? Ta có EM //AC ; EM= AC ( vì cùng bằng 2DM) Nên: AEMC là hình bình hành. Tứ giác AEBM là hình thoi vì:AEBM là hình bình hành có hai đường chéo cắt nhau tại trung điểm của mỗi đường.Hình bình hành AEBM có AB^EM nên là hình thoi. D.Hoạt động 4: Hướng dẫn về nhà _Về nhà học bài và làm bài tập 89c,d ,90 SGK trang 111,112 Xem lại các bài đã giải. Oân tập thật tốt để tiết sau kiểm tra 1 tiết. Hướng dẫn bài 89 câu d. E. Hoạt động 5:Nhận xét,xếp loại tiết học . IV.RÚT KINH NGHIỆM:
Tài liệu đính kèm:
 24.doc
24.doc





