Giáo án Hình học Lớp 7 - Tiết 65: Luyện tập - Năm học 2004-2005
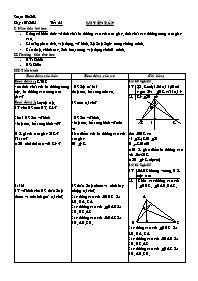
Hoạt động của thầy Hoạt động của trò Ghi bảng
Hoạt động 1: KTBC
Nêu tính chất của ba đường trung trực, ba đường cao trong tam giác?
Hoạt động 2: Luyện tập.
GV cho HS nêu GT, KL?
Cho 1 HS lên vẽ hình
Nhận xét, bổ sung hình vẽ?
M là gì của tam giác INK?
Vì sao?
=>IM như thế nào với KN?
Bài 61
GV vẽ hình cho HS thảo luận nhóm và nếu kết quả tại chỗ.
Bài 62
GV hướng dẫn HS cách vẽ hình.
Để chứng minh tam giác ABC cân (dự đoán tại đâu?) ta phải chúng minh được điều gì?
Muốn vậy ta phải chứng minh điều gì?
Hai tam giác này là tam giác gì? Ta chứng minh bằng nhau theo trường hợp nào?
GV cho HS thảo luận nhóm và đại diện lên trình bày.
Nhận xét (bổ sung nếu có)?
Tương tự vì tam giác đều là tam giác cân tại mấy đỉnh?
Về vận dụng chứng minh trên chứng minh phần còn lại.
1 HS lện trả bài
nhận xét, bổ sung nếu có.
HS nêu tại chỗ
1 HS lên vẽ hình.
Nhận xét, bổ sung hình vẽ nếu có
Giao điểm của ba đường cao của tam giác
IMNK
HS thảo luận nhóm và trình bày miệng tại chỗ.
Các đừng cao của HBC là:
AH, BA, CA
Các đường cao của HAB là:
CH, BC, AC
Các đường cao của HAC là:
BH, AB, CB.
HS vẽ hình
AB = AC hoặc góc B = góc C
BMC = CNB
Vuông
Cạnh huyền cạnh góc vuông.
HS thảo luận nhóm, đại diện lện trình bày.
Nhận xét, bổ sung nếu có. Bài 60 Sgk/83.
GT I, J, Kd; ld tại J; Ml
c qua I và MK cắt l tại N
KL KNIM N
l
M
I J K
Xét INK có
NJIK; KMIN
INKM=M
=>M là giao điểm ba đường cao củaINK
=>IMNK (đpcm)
Bài 61 Sgk/83
GT ABC không vuông. H là
trực tâm
KL Chỉ ra các đường cao của
HBC , HAB, HAC.
A
H
B C
Các đừng cao của HBC là:
AH, BA, CA
Các đường cao của HAB là:
CH, BC, AC
Các đường cao của HAC là:
BH, AB, CB.
Bài 62 Sgk/83
A
N M
B C
Chứng minh
Xét BMC và CNB có
Cạnh huyền BC chung
BM = CN (gt)
=>BMC = CNB (ch-cgv)
=>B = C
=>ABC cân tại A (đpcm)
Soaùn: 06/5/AÙ Daùy : 07/5/05 Tieỏt 65 LUYEÄN TAÄP I. Muùc tieõu baứi hoùc Cuỷng coỏ kieỏn thửực veà tớnh chaỏt ba ủửụứng cao cuỷa tam giaực, tớnh chaỏt caực ủửụứng trong tam giaực caõn. Kú naờng phaõn tớch, vaọn duùng, veừ hỡnh, laọp luaọn loõgớc trong chửựng minh. Caồn thaọn, chớnh xaực, linh hoaùt trong vaọn duùng chửnf1 minh. II. Phửụng tieọn daùy hoùc GV: ẹddh HS: ẹdht III. Tieỏn trỡnh Hoaùt ủoọng cuỷa thaày Hoaùt ủoọng cuỷa troứ Ghi baỷng Hoaùt ủoọng 1: KTBC Neõu tớnh chaỏt cuỷa ba ủửụứng trung trửùc, ba ủửụứng cao trong tam giaực? Hoaùt ủoọng 2: Luyeọn taọp. GV cho HS neõu GT, KL? Cho 1 HS leõn veừ hỡnh Nhaọn xeựt, boồ sung hỡnh veừ? M laứ gỡ cuỷa tam giaực INK? Vỡ sao? =>IM nhử theỏ naứo vụựi KN? Baứi 61 GV veừ hỡnh cho HS thaỷo luaọn nhoựm vaứ neỏu keỏt quaỷ taùi choó. Baứi 62 GV hửụựng daón HS caựch veừ hỡnh. ẹeồ chửựng minh tam giaực ABC caõn (dửù ủoaựn taùi ủaõu?) ta phaỷi chuựng minh ủửụùc ủieàu gỡ? Muoỏn vaọy ta phaỷi chửựng minh ủieàu gỡ? Hai tam giaực naứy laứ tam giaực gỡ? Ta chửựng minh baống nhau theo trửụứng hụùp naứo? GV cho HS thaỷo luaọn nhoựm vaứ ủaùi dieọn leõn trỡnh baứy. Nhaọn xeựt (boồ sung neỏu coự)? Tửụng tửù vỡ tam giaực ủeàu laứ tam giaực caõn taùi maỏy ủổnh? Veà vaọn duùng chửựng minh treõn chửựng minh phaàn coứn laùi. 1 HS leọn traỷ baứi nhaọn xeựt, boồ sung neỏu coự. HS neõu taùi choó 1 HS leõn veừ hỡnh. Nhaọn xeựt, boồ sung hỡnh veừ neỏu coự Giao ủieồm cuỷa ba ủửụứng cao cuỷa tam giaực IMNK HS thaỷo luaọn nhoựm vaứ trỡnh baứy mieọng taùi choó. Caực ủửứng cao cuỷa HBC laứ: AH, BA, CA Caực ủửụứng cao cuỷa HAB laứ: CH, BC, AC Caực ủửụứng cao cuỷa HAC laứ: BH, AB, CB. HS veừ hỡnh AB = AC hoaởc goực B = goực C BMC = CNB Vuoõng Caùnh huyeàn caùnh goực vuoõng. HS thaỷo luaọn nhoựm, ủaùi dieọn leọn trỡnh baứy. Nhaọn xeựt, boồ sung neỏu coự. Baứi 60 Sgk/83. GT I, J, Kd; ld taùi J; Ml c qua I vaứ MK caột l taùi N KL KNIM N l M I J K Xeựt INK coự NJIK; KMIN INKM=M =>M laứ giao ủieồm ba ủửụứng cao cuỷaINK =>IMNK (ủpcm) Baứi 61 Sgk/83 GT ABC khoõng vuoõng. H laứ trửùc taõm KL Chổ ra caực ủửụứng cao cuỷa HBC , HAB, HAC. A H B C Caực ủửứng cao cuỷa HBC laứ: AH, BA, CA Caực ủửụứng cao cuỷa HAB laứ: CH, BC, AC Caực ủửụứng cao cuỷa HAC laứ: BH, AB, CB. Baứi 62 Sgk/83 A N M B C Chửựng minh Xeựt BMC vaứ CNB coự Caùnh huyeàn BC chung BM = CN (gt) =>BMC = CNB (ch-cgv) =>B = C =>ABC caõn taùi A (ủpcm) Hoaùt ủoọng 3: Daởn doứ Veà xem kú laùi lyự thuyeỏt vaứ caực daùng baứi taọp ủaừ laứm. Xem laùi toaứn boọ lyự thuyeỏt cuỷa chửụng tieỏt sau oõn taọp chửụng. BTVN: 63, 64, 65 Sgk/87 OÂn caực caõu hoỷi lyự thuyeỏt.
Tài liệu đính kèm:
 TIET65.doc
TIET65.doc





