Giáo án Hình học Lớp 7 - Tiết 27: Luyện tập 2 - Năm học 2008-2009
Hoạt động 1:KTBC.
Gv treo bảng phụ bài 30/91.
Gv cho 1 học sinh đọc to đè bài và gọi 1 em lên bảng giải thích.
Hoạt động 2: Luyện tập:
Gv cho học sinh đọc đề và vẽ hình bài 31/120.
-Thế nào là trung trực của một đoạn thẳng?
- Để chứng minh MA=MB ta phải chứng minh điều gì?
-Gv cho cho học sinh đọc đề bài 32/120.
Giáo viên vẽ hình.
-Vì sao BH là phân giác của góc ABK?
-Hãy chứng minh các tam giác ABH và BHK bằng nhau?
Vì góc ABC không xen giữa hai cạnh AC và BC.Góc ABC không xen giữa hai cạnh BC và CA. Do đó không thể sử dụng được trường hợp cgc.
Học sinh trả lời.
-Học sinh đọc đề.
- BH là phân giác của góc ABK vì hai tam giác ABH và BHK bằng nhau.
Bài 30/ 91:
Các ABC và ABC không xen giữa các cạnh bằng nhau.
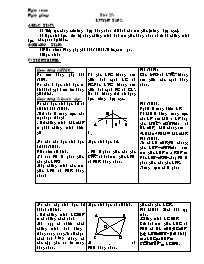
Bài 31/120.
Gọi H là trung điểm AB.
Vì MH là đường trung trực của AB nên MH AB hay góc MHA =MHB=1v và HA =HB, MH chung nên
AHM=BHMMA=MB.
Bài 32/120.
-Ta có AH =HK;BH chung; góc AHB =BHK=1v nên tam giác AHB = KHB Góc ABH =KBH hay BH là phân giác của góc ABK.
-Tương tự ta có là phân
Ngày soạn: Ngày giảng: Tiết 27: LUYệN TậP 2. A/MụC TIêU: 1/ Tiếp tục củng cố trường hợp bằng nhau thứ hai của tam giác (trường hợp cgc). 2/ Học sinh được rèn kỹ năng chứng minh hai tam giác bằng nhau và từ đó chứng minh được các quan hệ khác. B/PHươNG TIệN: 1/Giáo viên: Bảng phụ ghi bài 30/120.Thước,com pa. 2/Học sinh: C/TIếN TRìNH: Hoạt động 1:KTBC. Gv treo bảng phụ bài 30/91. Gv cho 1 học sinh đọc to đè bài và gọi 1 em lên bảng giải thích. Hoạt động 2: Luyện tập: Gv cho học sinh đọc đề và vẽ hình bài 31/120. -Thế nào là trung trực của một đoạn thẳng? - Để chứng minh MA=MB ta phải chứng minh điều gì? -Gv cho cho học sinh đọc đề bài 32/120. Giáo viên vẽ hình. -Vì sao BH là phân giác của góc ABK? -Hãy chứng minh các tam giác ABH và BHK bằng nhau? Vì góc ABC không xen giữa hai cạnh AC và BC.Góc A’BC không xen giữa hai cạnh BC và CA’. Do đó không thể sử dụng được trường hợp cgc. M A H B Học sinh trả lời. -Học sinh đọc đề. - BH là phân giác của góc ABK vì hai tam giác ABH và BHK bằng nhau. Bài 30/ 91: Các ABC và A’BC không xen giữa các cạnh bằng nhau. Bài 31/120. Gọi H là trung điểm AB. Vì MH là đường trung trực của AB nên MH ^ AB hay góc MHA =MHB=1v và HA =HB, MH chung nên DAHM=DBHMịMA=MB. Bài 32/120. -Ta có AH =HK;BH chung; góc AHB =BHK=1v nên tam giác AHB = D KHB ị Góc ABH =KBH hay BH là phân giác của góc ABK. -Tương tự ta có là phân -Gv cho chọ sinh đọc đề bài và vẽ hình. - Để chứng minh AC//DB ta có những cách nào? -Như vậy có nhiều cách chứng minh hai đường thẳng song song.Ta sẽ chọn cách hai đường thẳng có các cặp góc so le trong bằng nhau. Gv đọc đề bài và cho học sinh vẽ hình. -Gv yêu cầu học sinh ghi gt;kl. - Để chứng minh: DA=DB ta phải chứng minh điều gì? -Hãy chứng minh hai tam giác AOD và BOD bằng nhau? Từ hai tam giác bằng nhau ta có điều gì? Em có nhận xét gì về các góc ADO và góc BDO và? Vì sao chúng bằng nhau? -Học sinh đọc và vẽ hình. A B O C D -Hai tam giác AOC và BOD bằng nhau. Học sinh vẽ hình và ghi gt;kl. Gt D AOC: AO=BB. AOD=DOC. Kl a/ DA=DB. b/ OD ^ AB. Hai tam giác bằng nhau Học sinh chứng minh. -Học sinh nêu. -Ta có các cặp góc tương ứng bằng nhau. Bằứng nhau Cặp góc tương ứng giác của góc ACK. Bài 41/102 Sách bài tập toán. -Chứng minh AC //DB. Xét hai tam giác AOC và BOD có OA =OD;OC=OB (gt); AOC=BOD (đối đỉnh) ịDAOC=DDOBị ACO=ODB ị AC//BD. Bài 44/103sbt O A D B Chứng minh: a/ C/m DA=DB. Xét AOD và BOD có OA = OB (gt) OD chung; AOD=BOD (vì OD là phân giác của góc AOB) ị D AOD= D BOD ị AD=DB. b/ Vì D AOD= D BOD nên ADO =BDO mà ADO +BDO = 1800 ị ADO=BDO = 900 => OD ^ AB Hoạt động 3: Hướng dẫn về nhà. BTVN số 42;43/103. Về xem trước bài 5 tiết sau học Thực hiện vẽ bài toán Sgk /121 ? Khi nào thì hai tam giác bằng nhau theo trường hợp góc - cạnh-góc
Tài liệu đính kèm:
 Tiet 27.doc
Tiet 27.doc





