Đề thi khảo sát chọn nguồn học sinh giỏi môn Toán cấp THCS - Năm học 2006-2007
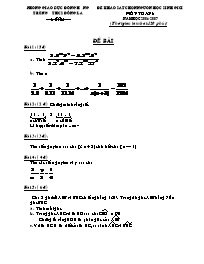
ĐỀ BÀI
Bài 1: (1,5 điểm)
Vẽ đồ thị hàm số y =
Bài 2: (1,5 điểm)
Tìm x; y biết và x10.y10 = 1024
Bài 3: (1,5 điểm)
Chứng minhnếu thì
Bài 4: (1,5 điểm)
Tìm giá trị nhỏ nhất của biểu thức A=
Bài 5: (1,5 điểm)
Cho đa thức P(x) =ã3 = bx2 =cx +d. với P(o)và P(1) là số nguyên lẻ. Chứng minh rằng p(x) không thể có nghiệm nguyên
Bài 6: (1,5 điểm)
Cho tam giác ABC có AB = AC góc BAC bằng 900 . D là một điểm thuộc cạnh BC gọi E là trung điểm của đoạn BD. Từ C kẻ tia vuông góc với AE tia này cắt AB ở K. Đường thẳng Dx vuông góc với CK cắt AC ở I cắt BA ở M
Chứng minh:
a/ AC làđường trung trực của BM
b/ AK = AI
c/ Tam giác MCK có 3 đường cao cắt nhau tại I
Bạn đang xem tài liệu "Đề thi khảo sát chọn nguồn học sinh giỏi môn Toán cấp THCS - Năm học 2006-2007", để tải tài liệu gốc về máy bạn click vào nút DOWNLOAD ở trên
Phòng Giáo dục Đông Hư ng
Tr ường THCS ĐÔNg la
ắ&ắ
đề khảo sát chọn nguồn Học sinh giỏi
Môn Toán 6
năm học 2006-2007
(Thời gian làm bài:120 phút)
đề bài
Bài 1: (5đ)
Tính
Tìm x
Bài 2: (2 đ) Chứng minh rằng số.
11 1 2 11 1
n chữ số n chữ số
Là hợp số với mọi n
Bài 3: (3 đ).
Tìm số nguyên n sao cho ( 3 n + 2) chia hết cho ( n – 1)
Bài 4: ( 4 đ)
Tìm các số nguyên x và y sao cho
Bài 5: ( 6 đ)
Cho 2 góc kề A0B và B0C có tổng bằng 160 0. Trong đó góc A0B bằng 7 lần góc B0C
Tính mỗi góc
Trong góc A0C vẽ tia 0D sao cho C0D= 900
Chứng tỏ rằng 0D là tia phân giác của A0B
c. Vẽ tia 0C’ là tia đối của tia 0C, so sánh A0C và B0C’
Biểu điểm toán 6
Nội dung
Điểm
Bài 1: (5đ)
a. ( 2đ)
b. (3đ)
Vậy
Rút ra:
Tìm được: x = 305
Bài 2: ( 2 đ)
11 1 2 11 1 = 11 1 00 0 + 11 1
n chữ số n chữ số n + 1 n n+1
= 11 1 . 10n + 11 1
n +1 n + 1
= 11 1 . (10n + 1)
n +1
Số đã cho được viết thành tích của 2 thừa số lớn hơn 1 .Vậy nó là hợp số.
1,0
1,0
1,0
Bài 3: ( 3 đ)
( 3 n + 2) ( n – 1)
Suy ra được 5 ( n – 1)
n – 1 ư ( 5)
ư ( 5) = -5 ; -1; 1; 5
Lập bảng tìm được n - 4 ; 0; 2 ; 6
1,0
1,0
1,5
0,5
Bài 4: ( 4 đ)
x. ( 2y + 1) = 30 nên 2y + 1 là ước lẻ của 30
Lập bảng: Tìm được x ; y
Trả lời: ( 8 cặp)
Bài 5 ( 6 đ) B D
C
0 A
2,0
1,0
1,0
C’
Tính được A0B = 140 0 ; B0C= 20 0
Tính được A0D = 70 0
B0D = 70 0
0,5
Chỉ ra được tia 0D nằm giữa hai tia 0A; 0B
và A0D ,B0D =(70 0 )
1,0
c. Tính được B0C’= 160 00,5
Kết luận: A0C = B0C (= 1600)
(1,0)
(1,0)
1,0
1,0
1,0
0,5
0,5
0,5
0,5
Phòng Giáo dục Đông Hư ng
Trường THCS ĐÔNg la
ắ&ắ
đề khảo sát chọn nguồn Học sinh giỏi
Môn Toán 7
năm học 2006-2007
(Thời gian làm bài: 120 phút)
đề bài
Bài 1: (1,5 điểm)
Vẽ đồ thị hàm số y =
Bài 2: (1,5 điểm)
Tìm x; y biết và x10.y10 = 1024
Bài 3: (1,5 điểm)
Chứng minhnếu thì
Bài 4: (1,5 điểm)
Tìm giá trị nhỏ nhất của biểu thức A=
Bài 5: (1,5 điểm)
Cho đa thức P(x) =ã3 = bx2 =cx +d. với P(o)và P(1) là số nguyên lẻ. Chứng minh rằng p(x) không thể có nghiệm nguyên
Bài 6: (1,5 điểm)
Cho tam giác ABC có AB = AC góc BAC bằng 900 . D là một điểm thuộc cạnh BC gọi E là trung điểm của đoạn BD. Từ C kẻ tia vuông góc với AE tia này cắt AB ở K. Đường thẳng Dx vuông góc với CK cắt AC ở I cắt BA ở M
Chứng minh:
a/ AC làđường trung trực của BM
b/ AK = AI
c/ Tam giác MCK có 3 đường cao cắt nhau tại I
đáp án và biểu điểm
Bài 1: (1,5 điểm)
Viết được x nếu x 0
-x nếu x< 0 (0,5 điểm)
Do đó đồ thị hàm số là tia phân giác của góc phần tư thứ I và thứ II (0,5 điểm)
Vẽ đúng (0,5 điểm)
Bài 2: (1,5 điểm)
Viết được =>y2 = 4x2 (0,5 điểm)
Thay y2 = 4x2 vao x10.y10 =1024 =>x20 = 1 (0,5 điểm)
Giải ra 4 cặp giá trị (x =1; y =2); (x=1; y=-2); (x=-1; y=2); (x=-1; y=-2)
(0,5 điểm)
Bài 3: (1,5 điểm)
Suy ra (1 điểm)
Kết luận : (0,5 điểm)
Bài 4: (1,5 điểm)
Viết được khi x-2007 và 2-x cùng dấu (0,5 điểm)
Lập bảng xét dấu và kết luận 2 x 102
A nhỏ nhất = 2005 (0,5 điểm)
Bài 5: (1,5 điểm)
P(1) = a + b + c + d Giả sử mZ mà P(m) = 0
M chẵn => – P (0) chẵn (0,5 điểm)
M lẻ => P(1) chẵn (0,5 điểm)
Tập hợp và kết luận (0,5 điểm)
Bài 6: (2,5 điểm)
Vẽ hình GT ; KL đúng (0,5 điểm)
a/ (0,5 điểm)
b/ CM 2 tam giác AIB và AKC bằn nhau => AK = AI (1 điểm)
c/ Chỉ ra mi và AC của tam giác MCK gặp nhau tại I => đường cao thứ ba cũng đi qua I (1 điểm)
Phòng Giáo dục Đông Hư ng
Trư ờng THCS ĐÔNg la
ắ&ắ
đề khảo sát chọn nguồn Học sinh giỏi
Môn Toán 8
năm học 2006-2007
(Thời gian làm bài: 120 phút)
Bài 1: (5 điểm)
Cho K =
a/ Tìm điều kiện xác định của K
b/ Rút gọn K
c/ Với giá trị nào của x thì K > 0
d/ Tìm giá trị nguyên của x để K có giá trị nguyên
Bài 2: (2 điểm)
Chứng minh tích của bốn số nguyên liên tiếp cộng với 1 là một số chính phương ?
Bài 3: Giải phương trình (4 điểm)
a/ 8(x2 + ) - 34(x + ) + 51 = 0
b/ x5 +2x4 + 3x3 + 3x2 + 2x = -1
Bài 4: (3 điểm)
a/ Cho: + + = 0 và a; b; c là 3 số khác nhau
Chứng minh rằng:
+ + = 0
b/ Cho a; b > 0 Chứng minh
a4 + b4 ab(a2 + b2)
Bài 5: (4 điểm)
Cho hình vuông ABCD; Trên cạnh AB lấy điểm M; Trên tia đối của tia CB lấy điểm N sao cho AM = CN . Gọi E là trung điểm của MN; Tia DE cắt BC tại F. Qua M vẽ đường thẳng song song với AD cắt DF tại H.
Chứng minh
a/ Tứ giác MFNH là hình thoi
b/ ND2 = NB . NF
c/ Chu vi tam giác BMF không đổi khi M di chuyển trên cạnh AB
Bài 6 (2 điểm)Cho tam giác ABC; phân giác AE (EBC)
Chứng minh AB.AC > AE2
Đáp án và biểu điểm
Bài 1: (5 điểm)
Câu a/(1 điểm) Giải: x - 1 0 (0,25 điểm)
x3 + x - x2 - 1 0 (0,5 điểm)
ĐKXĐ của K x 1 (0,25 điểm)
Câu b/ K = (2 điểm)
Câu c/ Nêu ĐKXĐ của K x 1 (0,25 điểm)
K > 0 ú x > 1 (0,5 điểm) ;
Kết luận: K > 0 ú x > 1 (0,25 điểm)
Câu d/ (2 điểm)
ĐKXĐ của K x > 0 (0,25 điểm)
K có giá trị nguyên: Giải được x = 2 ; x = 0 (0,25 điểm)
Kết luận : Với x = 0; x = 2 ; x 1 thì K có giá trị nguyên (0,25 điểm)
Bài 2 (2 điểm)
Gọi 4 số nguyên liên tiếp lần lượt là n; n = 1; n + 2; n + 3 (n Z) (0,5 điểm)
Theo bài ra ta có:
n(n + 1)(n + 2)(n + 3) + 1 = (n2 + 3n)(n2 + 3n + 2) (0,75 điểm)
Đặt m = n2 + 3n (0,25 điểm)
Tìm ra m(m + 2) + 1 = (m + 1)2 (0,5 điểm)
Kết luận (0,25 điểm)
Bài 3: (4 điểm)
a/ (2 điểm) Tập nghiệm của phương trình S = { 2; }
b/ (2 điểm) Tập nghiệm của phương trình S = {- 1 }
Bài 4: (3 điểm)
a/ (2 điểm)
Vì + + = 0 => = ... = (1) (0,75 điểm)
Nhân 2 vế của (1 )với
= (0,5 điểm)
Tương tự với ; (0,5 điểm)
Cộng 3 vế => ĐPCM (0,25 điểm)
Bài 5: (4 điểm)
Vẽ hình ghi GT; KL đúng (0,5 điểm)
Câu a/ (1,5 điểm)
Câu b/ (1,5 điểm)
Câu c/ (0,5 điểm)
Bài 6:(2 điểm)
Vẽ hình ghi GT; KL đúng (0,5 điểm)
Vẽ được yếu tố phụ EF sao cho góc AEF = góc B (0,5 điểm)
Chứng minh tam giác ABE đồng dạng với tam giác AEF (g -g)
=> (0,5 điểm)
Lập luận F AC => à < AC
AE2 < AB.AC
Phòng Giáo dục Đông Hư ng
Trư ờng THCS ĐÔNg la
ắ&ắ
đề khảo sát chọn nguồn Học sinh giỏi
Môn Toán 9
năm học 2006-2007
(Thời gian làm bài: 120 phút)
đề bài
Bài 1: Tìm 4 số tự nhiên liên tiếp , biết rằng tích của 4 số đó bằng 3024
Bài 2 : a. Cho biểu thức
Rút gọn B
Tính giá trị của B khi x = 3 +
Chứng minh rằng B<=1 với mọi giá trị của x 0 và x
Bài 3: Giả hệ phương trình
( x- y)(x2+y2) = 5
( x+ y) (x2-y2) = 9
Bài 4: Cho hàm số:
y =
a. Tìm khoảng xác định của hàm số y
b. Tính giá trị lớn nhất của y và các giá trị tương ứng của x trong khoảng xác định đó.
Bài 5:
Cho đường tròn tâm 0, bán kính R và 2 đường kính AB và CD tiếp tuyến tại A của đường tròn tâm ( 0 ) cắt các đường thẳng BC và BD tại 2 điểm tương ứng là E và F . Gọi P, Q lần lượt là trung điểm của các đoạn thẳng EA và AF.
a. Chứng minh rằng trực tâm H của BQP là trung điểm của đoạn thẳng 0A
b. Hai đường kính AB và CD có vị trí tương đố như thế nào thì BQP có diện tích nhỏ nhất? Hãy tính diện tíchnhỏ nhất đó theo R
Biểu điểm toán 9
Nội dung
Điểm
Bài 1:(3 đ)
Gọi x là số tự nhiên đầu tiên thì các số tự nhiên liên tiếp là x+ 1 ; x + 2
; x+ 3 ; x
Theo bào ra ta có phương trình
x (x+1)(x+2)(x+3)=3024
- Giải phương trình
(x2+3x)(x2+3x+2)= 3024
Đặt x2+3x= X (X>0) ta có X2+ 2X- 3024 = 0
X1= 54; X2 = - 56 (loại)
Giải phương trình x2 + 3x = 54
x = 6; x = -9( loại)
Các số phải tìm là: 6 ; 7 ; 8 ; 9
Bài 2: ( 3 đ)
a. Rút gọn số bị chia ta được Rút gọn số chia ta được
Thực hiện phép chia B =
b. Tính
B =
c. Với x ta có (
Vì x + 4 >0 nên Dấu “ =” xảy ra khi x = 4
Bài 3: Khai riển từng phương trình từng vế với vế
( 1)
xy = 2(x – y)
Hệ (I) x – y =
x – y =
Từ ( 1) và ( 2) Kết hợp với pt (1) và ( -1; - 2)
Bài 4: ( 3 đ)
a. XĐ:
x2 + 1
2x 2 – 4
21 – 3 x2
b. áp dụng bất đẳng thức Bunhiacôpxky
= tại x =
Bài 5: ( 8 đ)
0
B
B
D
C
E P A Q F
a. đặt AE = a ; AF = b
; trong tam giác vuông BEF có AB2 =A E . AF
= ab
Dựng PI là trực tâm
AH = là trung điểm 0A
b. S BPQ min vì PQ =
PQ min a + b min Có ab = 4 R2 không đổi
( Cô si) a+ b
(a+b) nhỏ nhất
nhỏ nhất = 2 R
BEF vuông cân BCD cũng vuông cân
Vậy khi AB thì nhỏ nhất = 2R2
1,0
1,0
1,0
1,0
1,0
1,0
1,0
1,0
1,0
1,0
2,0
4,0
Tài liệu đính kèm:
 de thi hoc sinh gioi yoan 6 DA IN.doc
de thi hoc sinh gioi yoan 6 DA IN.doc





