Đề kiểm tra học kỳ II môn Toán Lớp 9 - Phạm Thị Thanh Phương

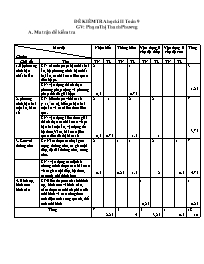
ĐỀ KIỂM TRA học kì II Toán 9
GV: Phạm Thị Thanh Phương
A. Ma trận đề kiểm tra
 Mức độ
Chuẩn
Nhận biết
Thông hiểu
Vận dụng ở cấp độ thấp
Vận dụng ở cấp độ cao
Tổng
Chủ đề
Tên
TN
TL
TN
TL
TN
TL
TN
TL
1.Hệ phương trình bậc nhất hai ẩn
KT: nắm được pt bậc nhất hai ẩn, hệ phương trình bậc nhất hai ẩn, các bài toán liên quan đến hệ pt.
2
0,5
1
0.75
3
1.25
KN: vận dụng thành thạo phương pháp cộng và phương pháp thế để giải hệ pt
2. phương trình bậc hai một ẩn, hàm số
KT: hiểu được về hàm số y=ax2(a¹0), hiểu pt bậc hai một ẩn và các kiến thức liên qua.
2
 0,5
1
0.75
2
1.5
2
1
7
3,75
KN: vận dụng kiến thức giải thành thạo các bài toán về pt bậc hai một ẩn, vận dụng tốt hệ thức Vi et, bài toán liên quan đến đồ thị hàm số
3. Góc với đường tròn
Kt: Nắm được các loại góc trong đường tròn, tứ giác nội tiếp, độ dài đường tròn, cung tròn.
2
0.5
1
0.25
1
1.5
2
2
1
0.5
7
4.75
KN : vận dụng các định lí chứng minh được các bài toán về tứ giác nội tiếp, hệ thức, các tính chất hình học
4. Hình trụ, hình nón hình cầu
KT:Hiểu được cách sinh hình trụ, hình nón và hình cầu, nắm được các thành phần của mỗi hình và các công thức tính diện tích xung quanh, thể tích mỗi hình
1
0,25
1
0.25
Tổng
7
2.25
5
4
5
 3,25
1
 0.5
18
 10
B. ĐỀ BÀI
I. TRẮC NGHIỆM(2Đ)
Chọn chữ cái đứng trước đáp án đúng
Câu 1. Nghiệm của hệ phương trình 
A. (-1;-2) 	B. (1;2) 	C. (-1;-6) 	D. (1;-6)
Câu 2. Phương trình nào dưới đây có thể kết hợp với phương trình x + y = 1 để được hệ phương trình có nghiệm duy nhất?
	A. y = -x +1	B. 0x + y = 1	C. x + y = 2	D. 3y = -3x+3
Câu 3: Hàm số 
Đồng biến với mọi x C. Nghịch biến với mọi x
Nghịch biến khi x 0 
Câu 4: Phương trình 3x2 - a.x + b = 0 có 2 nghiệm là x1, x2 thì tổng x1+x2 là :
 	 A. -a/ 3 B. a/3 C. b/3 D. -b / 3
Câu 5: Cho hình vẽ: AC là đường kính. . Số đo là: 
A. 400 B. 45	 C. 600	D. 350
 Câu 6. Tứ giác ABCD là tứ giác nội tiếp, biết . Góc A và góc C có số đo lần lượt là
A. 1050 và 750 	B. 600 và 300 	C. 1000 và 800 	D. 1000 và 700
Câu 7: Cho đường tròn (O; 3 cm). Số đo cung PQ 
của đường tròn này là: 1200. Độ dài cung nhỏ PQ bằng:
 A. p cm B. 2p cm C. 1,5p cm D. 2,5p cm 
Câu 8: Cho hình chữ nhật ABCD có AB = 4cm, BC = 5cm. 
Quay hình chữ nhật đó một vòng cạnh AB được một hình trụ. Thể tích hình trụ đó là: 
 A. 100 p cm3 B. 80p cm3 C. 40p cm3 D. 60p cm3 
II. TỰ LUẬN(8đ)
Bài 1 (0,75đ): Giải hệ phương trình
 Bài 2:( 2,25đ)Cho phương trình : (1)
 a) Giải phương trình (1) với m = 2.
 b)Tìm m để phương trình (1)có hai nghiệm thỏa mãn 
Bài 3:(1đ)Cho hàm số y = 2x2
 a/ Vẽ đồ thị hàm số trên 
 b/ Tìm m để đường thẳng y = 4x + m tiếp xúc với đồ thị của hàm số y = 2x2 
Bài 4.(4đ)Cho đường tròn (O), đường kính AB, điểm I nằm giữa A và O sao cho AI = AO. Kẻ dây MN vuông góc với AB tại I. Gọi C là điểm tùy ý thuộc cung lớn MN sao cho C không trùng với M, N và B. 
Nối AC cắt MN tại E.
 a) Chứng minh tứ giác IECB nội tiếp được trong một đường tròn.
 b) Chứng minh ∆AME đồng dạng với ∆ACM và AM2 = AE.AC.
 c) Chứng minh AE.AC - AI.IB = AI2.
C. ĐÁP ÁN VÀ BIỂU ĐIỂM
I. Trắc nghiệm: mỗi câu đúng được 0,25đ
1
2
3
4
5
6
7
8
A
B
D
B
C
A
B
A
II. Tự luận
Bài 
Đáp án
Điểm
Bài 1(0,75đ)
Kết luận tập nghiệm
0,25đ
0,25đ
0,25đ
Bài2
(2,25đ)
a) (1đ)Cách 1: = 22 - 1.3 = 1
 = 1 
Vậy phương trình trên có 2 nghiệm phân biệt 
 x1 = 2-1 = 1 ; x2 = 2+ 1= 3 
Cách 2: x2 - x -3x + 3 = 0
 x(x-1)- 3(x- 1) = 0
 (x- 1 )(x - 3) = 0
 x - 1 = 0 hoặc x - 3 = 0 
 x = 1 hoặc x = 3
b)(1,25đ) Để pt (1)có hai nghiệm phân biệt khi > 0 hay = m2 - 2m + 1 > 0 > 0 m 1. 
 Gọi x1; x2 là 2 nghiệm của pt(1) theo Vi-Ét
 ta có : x1 + x2 = 2m; 
 x1.x2 = 2m - 1
 Mà x12 + x22 = 10 nên x12 + x22 = (x1 + x2)2 - 2x1.x2 = 10 hay (2m)2 - 2. (2m - 1) = 10 
 4m2 - 4m + 2 = 10 
 4m2 - 4m - 8 = 0 
 m2 - m - 2 = 0 
 (m- 2)(m + 1) = 0 
 m - 2 = 0 hoặc m + 1 = 0 
 m = 2 hoặc m = -1 
Vậy với m = 2; m =-1 thì pt(1) có hai nghiệm thỏa mãn x12 + x22 = 10.
0,5đ
0,5đ
0,25đ
0,25đ
0,25đ
0,25đ
0,25đ
Bài 3(1đ)
a) Hs vẽ đúng
b) Pt hoành độ giao điểm của đường thẳng y = 4x + m với đồ thị của hàm số y = 2x2 là:
4x+m = 2x22x2-4x-m = 0(1)
 = 4+2m
Để đt tiếp xúc với đồ thị hàm số y = 2x2 Pt (1) có nghiệm kép = 0 4+2m = 0 m = -2
Vậy m =-2 là giá trị cần tìm
0,5đ
0,25đ
0,25đ
Bài 4(4đ)
Hình vẽ đúng ,a 
A
B
M
E
C
I
O1
N
a.(1,5đ) , 
* (giả thiết) 
* (góc nội tiếp chắn nửa đường tròn) 
Suy ra + +900 = 1800
Kết luận: Tứ giác IECB là tứ giác nội tiếp(đl đảo của t/g nt)
b)(1đ) Ta có:
* sđ = sđ 
* 
*GócAchung,suyra∆AME ∆ACM. 
* Do đó: AM2 = AE.AC 
 c) (1đ)
* MI là đường cao của tam giác vuông MAB nên 
MI2 = AI.IB
* Trừ từng vế của hệ thức ở câu b) với hệ thức trên
* Ta có: AE.AC - AI.IB = AM2 - MI2 = AI2.
0,5đ
0,25đ
0,5đ
0,5đ
0,25đ
0,25đ
0,25đ
0,25đ
0,25đ
0,25đ
0,25đ
0,25đ
0,25đ
(HS làm theo cách khác đúng vẫn cho điểm tối đa)